Back

Poisson's Equation

Recall the Newton's law of universal gravitation:

F=−GMmr2r^,\boldsymbol{F} = - \frac{G M m}{r^2} \boldsymbol{\hat{r}},

where GG is the gravitational constant, MM is the mass of the source body, mm is the mass of the falling body and r^\boldsymbol{\hat{r}} is the unit vector pointing from MM to mm. Since we are using geometrized units, the above equation is:

F=−Mmr2r^,F=Mmr2. \begin{align*} \boldsymbol{F} &= - \frac{M m}{r^2} \boldsymbol{\hat{r}}, \\ F &= \frac{M m}{r^2}. \end{align*}

By F=ma\boldsymbol{F} = m \boldsymbol{a}, the gravitational acceleration (gravitational field denoted by g\boldsymbol{g}) is equal to:

g=−Mr2r^,g=Mr2. \begin{align*} \boldsymbol{g} &= - \frac{M}{r^2} \boldsymbol{\hat{r}}, \\ g &= \frac{M}{r^2}. \end{align*}
Newton's law of universal gravitation

The gravitational force is conservative:

∮CF⋅ds=0,\oint_C \boldsymbol{F} \cdot d\boldsymbol{s} = 0,

meaning the work is independent on the path taken and depends only on the initial and end point.

The potential energy is defined as the work done to move an object of mass mm from infinity to a distance rr. The work done by gravity

Wg=∫F⋅dr=−∫∞rF dr=Mm∫∞r−1r2=Mmlim⁡n→∞[1r]nr=Mmr. \begin{align*} W_g &= \int \boldsymbol{F} \cdot d\boldsymbol{r} \\ &= - \int_{\infty}^r F\ dr \\ &= M m \int_{\infty}^r -\frac{1}{r^2} \\ &= M m \lim_{n \to \infty} \left[\frac{1}{r}\right]_n^r \\ &= \frac{M m}{r}. \end{align*}

And the external work WeW_e is the negative work done by the gravity:

We=−W=−Mmr.W_e = - W = - \frac{M m}{r}.

The potential is equal to:

ϕ=Wem=−Mr.\phi = \frac{W_e}{m} = -\frac{M}{r}.

The negative gradient of the potential is the gravitational acceleration:

g=−∇ϕ.\boldsymbol{g} = -\nabla \phi.

The flux of the gravitational field

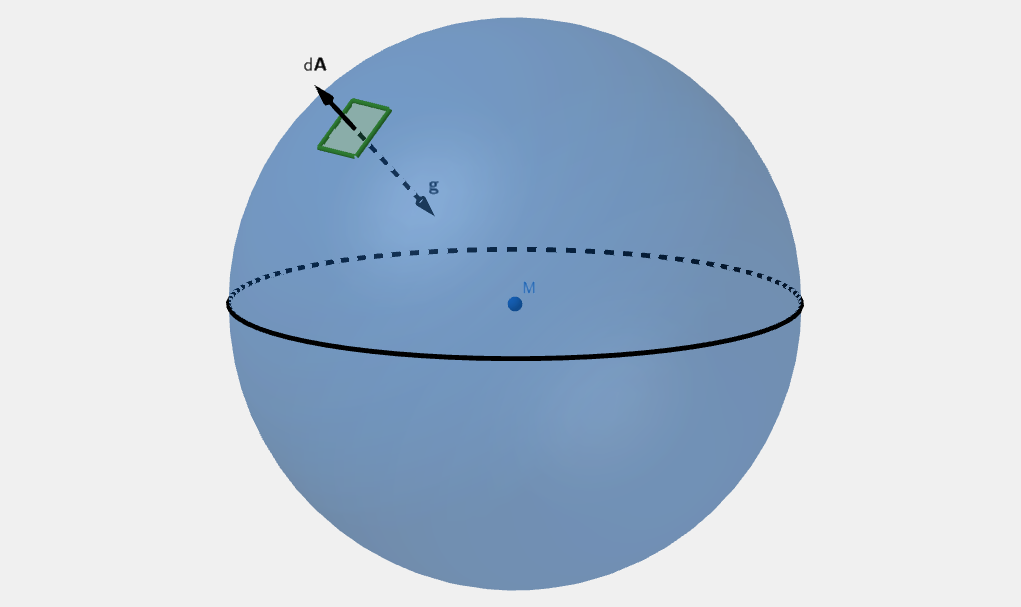
∯∂Vg⋅dA=−4πM.\oiint_{\partial V} \boldsymbol{g} \cdot d\boldsymbol{A} = - 4 \pi M.

For sphere, this would be:

Gauss's law illustration
∯∂Vg⋅dA=−∯∂Vg dA=−gA=−Mr24πr2=−4πM, \begin{align*} \oiint_{\partial V} \boldsymbol{g} \cdot d\boldsymbol{A} &= - \oiint_{\partial V} g\ dA \\ &= - g A \\ &= - \frac{M}{r^2} 4 \pi r^2 \\ &= - 4 \pi M, \end{align*}

where MM is mass enclosed by the surface ∂V\partial V. ∂V\partial V is the boundary surface of the volume VV.

By the divergence theorem:

∯∂Vg⋅dA=∭V(∇⋅g) dV=−4πM,∭V(∇⋅g) dV=∭V−4πρ dV,∇⋅g=−4πρ. \begin{align*} \oiint_{\partial V} \boldsymbol{g} \cdot d\boldsymbol{A} = \iiint_V (\nabla \cdot \boldsymbol{g})\ dV &= - 4 \pi M, \\ \iiint_V (\nabla \cdot \boldsymbol{g})\ dV &= \iiint_V - 4 \pi \rho \ dV, \\ \nabla \cdot \boldsymbol{g} &= - 4 \pi \rho. \end{align*}

Recall that gravitational acceleration is the negative gradient of the potential:

g=−∇ϕ.\boldsymbol{g} = -\nabla \phi.

If we substitute this into Gauss's law, we obtain Poisson's equation:

∇⋅g=−4πρ,∇⋅(−∇ϕ)=−4πρ,∇2ϕ=4πρ. \begin{align*} \nabla \cdot \boldsymbol{g} &= - 4 \pi \rho, \\ \nabla \cdot (- \nabla \phi) &= - 4 \pi \rho, \\ \nabla^2 \phi &= 4 \pi \rho. \end{align*}