Back Covariant Derivative Covariant derivative is a way to understand the rate of change of tensor fields that takes into account changing basis vectors.
In flat space, the covariant derivative of a vector v \boldsymbol{v} v
∂ v ∂ x μ = ∂ ∂ x μ ( v ν e ν ) = ∂ v ν ∂ x μ e ν + v ν ∂ e ν ∂ x μ . \begin{align*} \frac{\partial \boldsymbol{v}}{\partial x^{\mu}} &= \frac{\partial}{\partial x^{\mu}} (v^{\nu} \boldsymbol{e_{\nu}}) \\ &= \frac{\partial v^{\nu}}{\partial x^{\mu}} \boldsymbol{e_{\nu}} + v^{\nu} \frac{\partial \boldsymbol{e_{\nu}}}{\partial x^{\mu}}. \end{align*} ∂ x μ ∂ v = ∂ x μ ∂ ( v ν e ν ) = ∂ x μ ∂ v ν e ν + v ν ∂ x μ ∂ e ν . In the previous chapter , we expressed partial derivative of basis vectors as follows:
∂ e ν ∂ x μ = Γ σ μ ν e σ + L μ ν n ^ , \frac{\partial \boldsymbol{e_{\nu}}}{\partial x^{\mu}} = \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}} + L_{\mu \nu} \boldsymbol{\hat{n}}, ∂ x μ ∂ e ν = Γ σ μν e σ + L μν n ^ , since we are dealing with flat space, the normal components are zero:
∂ e ν ∂ x μ = Γ σ μ ν e σ , \frac{\partial \boldsymbol{e_{\nu}}}{\partial x^{\mu}} = \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}}, ∂ x μ ∂ e ν = Γ σ μν e σ , substituting into the previous equation:
∂ v ∂ x μ = ∂ v ν ∂ x μ e ν + v ν Γ σ μ ν e σ = ∂ v σ ∂ x μ e σ + v ν Γ σ μ ν e σ = ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) e σ , \begin{align*} \frac{\partial \boldsymbol{v}}{\partial x^{\mu}} &= \frac{\partial v^{\nu}}{\partial x^{\mu}} \boldsymbol{e_{\nu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}} \\ &= \frac{\partial v^{\sigma}}{\partial x^{\mu}} \boldsymbol{e_{\sigma}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}} \\ &= \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{e_{\sigma}}, \end{align*} ∂ x μ ∂ v = ∂ x μ ∂ v ν e ν + v ν Γ σ μν e σ = ∂ x μ ∂ v σ e σ + v ν Γ σ μν e σ = ( ∂ x μ ∂ v σ + v ν Γ σ μν ) e σ , or, expressing as components:
∇ μ v σ = v σ ; μ = ∂ v σ ∂ x μ + v ν Γ σ μ ν , \nabla_{\mu} v^{\sigma} = v^{\sigma}{}_{;\mu} = \frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}, ∇ μ v σ = v σ ; μ = ∂ x μ ∂ v σ + v ν Γ σ μν , where ∇ μ v σ = v σ ; μ \nabla_{\mu} v^{\sigma} = v^{\sigma}{}_{;\mu} ∇ μ v σ = v σ ; μ σ \sigma σ v \boldsymbol{v} v μ \mu μ
As an example, consider the following vector field in Cartesian coordinates:
v = 1 2 e x + 1 2 e y . \boldsymbol{v} = \frac{1}{2} \boldsymbol{e_x} + \frac{1}{2} \boldsymbol{e_y}. v = 2 1 e x + 2 1 e y . The covariant derivative components are equal to zero:
v σ ; μ = ∂ v σ ∂ x μ + v ν Γ σ μ ν = 0 + v ν ⋅ 0 = 0. \begin{align*} v^{\sigma}{}_{;\mu} &= \frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu} \\ &= 0 + v^{\nu} \cdot 0 \\ &= 0. \end{align*} v σ ; μ = ∂ x μ ∂ v σ + v ν Γ σ μν = 0 + v ν ⋅ 0 = 0. But when we consider the following vector field with same components but in polar coordinates:
v = 1 2 e r + 1 2 e r . \boldsymbol{v} = \frac{1}{2} \boldsymbol{e_r} + \frac{1}{2} \boldsymbol{e_r}. v = 2 1 e r + 2 1 e r . Recall the nonzero Christoffel symbols:
Γ θ θ r = − r , Γ r θ θ = Γ θ r θ = 1 r , \begin{align*} \Gamma^r_{\theta \theta} &= -r, \\ \Gamma^{\theta}_{r \theta} = \Gamma^{\theta}_{\theta r} &= \frac{1}{r}, \end{align*} Γ θθ r Γ r θ θ = Γ θ r θ = − r , = r 1 , and the nonzero covariant derivative components are equal to:
v σ ; μ = v ν Γ σ μ ν , v r ; θ = 1 2 Γ r θ θ = − r 2 , v θ ; θ = v θ ; r = 1 2 r . \begin{align*} v^{\sigma}{}_{;\mu} &= v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}, \\ v^r{}_{;\theta} &= \frac{1}{2} \Gamma^r{}_{\theta \theta} \\ &= -\frac{r}{2}, \\ v^{\theta}{}_{;\theta} = v^{\theta}{}_{;r} &= \frac{1}{2r}. \end{align*} v σ ; μ v r ; θ v θ ; θ = v θ ; r = v ν Γ σ μν , = 2 1 Γ r θθ = − 2 r , = 2 r 1 . So we can see, that constant components does not imply constant vector field.
The covariant derivative transforms like a tensor:
∂ v ∂ x μ = ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) e σ , ∂ x ~ λ ∂ x μ ∂ v ∂ x ~ λ = ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) ∂ x ~ λ ∂ x σ e ~ λ , ∂ x μ ∂ x ~ α ∂ x ~ λ ∂ x μ ∂ v ∂ x ~ λ = ∂ x μ ∂ x ~ α ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) ∂ x ~ λ ∂ x σ e ~ λ , δ α λ ∂ v ∂ x ~ λ = ∂ x μ ∂ x ~ α ∂ x ~ λ ∂ x σ ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) e ~ λ , ∂ v ∂ x ~ α = ∂ x μ ∂ x ~ α ∂ x ~ λ ∂ x σ v σ ; μ e ~ λ , v ~ λ ; α = ∂ x μ ∂ x ~ α ∂ x ~ λ ∂ x σ v σ ; μ . \begin{align*} \frac{\partial \boldsymbol{v}}{\partial x^{\mu}} &= \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{e_{\sigma}}, \\ \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\mu}} \frac{\partial \boldsymbol{v}}{\partial \tilde{x}^{\lambda}} &= \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \boldsymbol{\tilde{e}_{\lambda}}, \\ \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\mu}} \frac{\partial \boldsymbol{v}}{\partial \tilde{x}^{\lambda}} &= \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \boldsymbol{\tilde{e}_{\lambda}}, \\ \delta^{\lambda}_{\alpha} \frac{\partial \boldsymbol{v}}{\partial \tilde{x}^{\lambda}} &= \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{\tilde{e}_{\lambda}}, \\ \frac{\partial \boldsymbol{v}}{\partial \tilde{x}^{\alpha}} &= \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} v^{\sigma}{}_{;\mu} \boldsymbol{\tilde{e}_{\lambda}}, \\ \tilde{v}^{\lambda}{}_{;\alpha} &= \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} v^{\sigma}{}_{;\mu}. \\ \end{align*} ∂ x μ ∂ v ∂ x μ ∂ x ~ λ ∂ x ~ λ ∂ v ∂ x ~ α ∂ x μ ∂ x μ ∂ x ~ λ ∂ x ~ λ ∂ v δ α λ ∂ x ~ λ ∂ v ∂ x ~ α ∂ v v ~ λ ; α = ( ∂ x μ ∂ v σ + v ν Γ σ μν ) e σ , = ( ∂ x μ ∂ v σ + v ν Γ σ μν ) ∂ x σ ∂ x ~ λ e ~ λ , = ∂ x ~ α ∂ x μ ( ∂ x μ ∂ v σ + v ν Γ σ μν ) ∂ x σ ∂ x ~ λ e ~ λ , = ∂ x ~ α ∂ x μ ∂ x σ ∂ x ~ λ ( ∂ x μ ∂ v σ + v ν Γ σ μν ) e ~ λ , = ∂ x ~ α ∂ x μ ∂ x σ ∂ x ~ λ v σ ; μ e ~ λ , = ∂ x ~ α ∂ x μ ∂ x σ ∂ x ~ λ v σ ; μ . If we compute covariant derivative in the transfromed basis, we get:
v ~ λ ; α = ∂ v ~ λ ∂ x ~ α + v ~ ν Γ ~ λ α ν , \begin{align*} \tilde{v}^{\lambda}{}_{;\alpha} &= \frac{\partial \tilde{v}^{\lambda}}{\partial \tilde{x}^{\alpha}} + \tilde{v}^{\nu} \tilde{\Gamma}^{\lambda}{}_{\alpha \nu}, \end{align*} v ~ λ ; α = ∂ x ~ α ∂ v ~ λ + v ~ ν Γ ~ λ αν , and setting it equal with the previous equation:
∂ v ~ λ ∂ x ~ α + v ~ ν Γ ~ λ α ν = ∂ x μ ∂ x ~ α ∂ x ~ λ ∂ x σ ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) = ∂ x μ ∂ x ~ α ∂ x ~ λ ∂ x σ ( ∂ ∂ x μ ( ∂ x σ ∂ x ~ β v ~ β ) + ∂ x ν ∂ x ~ γ v ~ γ Γ σ μ ν ) = ∂ x μ ∂ x ~ α ∂ x ~ λ ∂ x σ ( ∂ x ~ ρ ∂ x μ ∂ ∂ x ~ ρ ( ∂ x σ ∂ x ~ β v ~ β ) + ∂ x ν ∂ x ~ γ v ~ γ Γ σ μ ν ) = ∂ x ~ λ ∂ x σ ( ∂ x μ ∂ x ~ α ∂ x ~ ρ ∂ x μ ( ∂ 2 x σ ∂ x ~ ρ ∂ x ~ β v ~ β + ∂ x σ ∂ x ~ β ∂ v ~ β ∂ x ~ ρ ) + ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ γ v ~ γ Γ σ μ ν ) = ∂ x ~ λ ∂ x σ ( δ α ρ ( ∂ 2 x σ ∂ x ~ ρ ∂ x ~ β v ~ β + ∂ x σ ∂ x ~ β ∂ v ~ β ∂ x ~ ρ ) + ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ γ v ~ γ Γ σ μ ν ) = ∂ x ~ λ ∂ x σ ( ∂ 2 x σ ∂ x ~ α ∂ x ~ β v ~ β + ∂ x σ ∂ x ~ β ∂ v ~ β ∂ x ~ α + ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ γ v ~ γ Γ σ μ ν ) = ∂ x ~ λ ∂ x σ ∂ 2 x σ ∂ x ~ α ∂ x ~ β v ~ β + ∂ x ~ λ ∂ x σ ∂ x σ ∂ x ~ β ∂ v ~ β ∂ x ~ α + ∂ x ~ λ ∂ x σ ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ γ v ~ γ Γ σ μ ν = ∂ x ~ λ ∂ x σ ∂ 2 x σ ∂ x ~ α ∂ x ~ β v ~ β + δ β λ ∂ v ~ β ∂ x ~ α + ∂ x ~ λ ∂ x σ ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ γ v ~ γ Γ σ μ ν = ∂ x ~ λ ∂ x σ ∂ 2 x σ ∂ x ~ α ∂ x ~ β v ~ β + ∂ v ~ λ ∂ x ~ α + ∂ x ~ λ ∂ x σ ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ β v ~ β Γ σ μ ν = ∂ x ~ λ ∂ x σ v ~ β ( ∂ 2 x σ ∂ x ~ α ∂ x ~ β + ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ β Γ σ μ ν ) + ∂ v ~ λ ∂ x ~ α , v ~ β Γ ~ λ α β = ∂ x ~ λ ∂ x σ v ~ β ( ∂ 2 x σ ∂ x ~ α ∂ x ~ β + ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ β Γ σ μ ν ) , Γ ~ λ α β = ∂ x ~ λ ∂ x σ ( ∂ 2 x σ ∂ x ~ α ∂ x ~ β + ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ β Γ σ μ ν ) = ∂ x ~ λ ∂ x σ ∂ x μ ∂ x ~ α ∂ x ν ∂ x ~ β Γ σ μ ν + ∂ x ~ λ ∂ x σ ∂ 2 x σ ∂ x ~ α ∂ x ~ β , \begin{align*} \frac{\partial \tilde{v}^{\lambda}}{\partial \tilde{x}^{\alpha}} + \tilde{v}^{\nu} \tilde{\Gamma}^{\lambda}{}_{\alpha \nu} &= \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \\ &= \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \left(\frac{\partial}{\partial x^{\mu}} \left(\frac{\partial x^{\sigma}}{\partial \tilde{x}^{\beta}} \tilde{v}^{\beta}\right) + \frac{\partial x^{\nu}}{\partial \tilde{x}^{\gamma}} \tilde{v}^{\gamma} \Gamma^{\sigma}{}_{\mu \nu}\right) \\ &= \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \left(\frac{\partial \tilde{x}^{\rho}}{\partial x^{\mu}} \frac{\partial}{\partial \tilde{x}^{\rho}} \left(\frac{\partial x^{\sigma}}{\partial \tilde{x}^{\beta}} \tilde{v}^{\beta}\right) + \frac{\partial x^{\nu}}{\partial \tilde{x}^{\gamma}} \tilde{v}^{\gamma} \Gamma^{\sigma}{}_{\mu \nu}\right) \\ &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \left(\frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial \tilde{x}^{\rho}}{\partial x^{\mu}} \left(\frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\rho} \partial \tilde{x}^{\beta}} \tilde{v}^{\beta} + \frac{\partial x^{\sigma}}{\partial \tilde{x}^{\beta}} \frac{\partial \tilde{v}^{\beta}}{\partial \tilde{x}^{\rho}}\right) + \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\gamma}} \tilde{v}^{\gamma} \Gamma^{\sigma}{}_{\mu \nu}\right) \\ &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \left(\delta^{\rho}_{\alpha} \left(\frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\rho} \partial \tilde{x}^{\beta}} \tilde{v}^{\beta} + \frac{\partial x^{\sigma}}{\partial \tilde{x}^{\beta}} \frac{\partial \tilde{v}^{\beta}}{\partial \tilde{x}^{\rho}}\right) + \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\gamma}} \tilde{v}^{\gamma} \Gamma^{\sigma}{}_{\mu \nu}\right) \\ &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \left(\frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\alpha} \partial \tilde{x}^{\beta}} \tilde{v}^{\beta} + \frac{\partial x^{\sigma}}{\partial \tilde{x}^{\beta}} \frac{\partial \tilde{v}^{\beta}}{\partial \tilde{x}^{\alpha}} + \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\gamma}} \tilde{v}^{\gamma} \Gamma^{\sigma}{}_{\mu \nu}\right) \\ &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\alpha} \partial \tilde{x}^{\beta}} \tilde{v}^{\beta} + \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \frac{\partial x^{\sigma}}{\partial \tilde{x}^{\beta}} \frac{\partial \tilde{v}^{\beta}}{\partial \tilde{x}^{\alpha}} + \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\gamma}} \tilde{v}^{\gamma} \Gamma^{\sigma}{}_{\mu \nu} \\ &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\alpha} \partial \tilde{x}^{\beta}} \tilde{v}^{\beta} + \delta^{\lambda}_{\beta} \frac{\partial \tilde{v}^{\beta}}{\partial \tilde{x}^{\alpha}} + \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\gamma}} \tilde{v}^{\gamma} \Gamma^{\sigma}{}_{\mu \nu} \\ &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\alpha} \partial \tilde{x}^{\beta}} \tilde{v}^{\beta} + \frac{\partial \tilde{v}^{\lambda}}{\partial \tilde{x}^{\alpha}} + \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\beta}} \tilde{v}^{\beta} \Gamma^{\sigma}{}_{\mu \nu} \\ &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \tilde{v}^{\beta} \left(\frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\alpha} \partial \tilde{x}^{\beta}} + \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\beta}} \Gamma^{\sigma}{}_{\mu \nu}\right) + \frac{\partial \tilde{v}^{\lambda}}{\partial \tilde{x}^{\alpha}}, \\ \tilde{v}^{\beta} \tilde{\Gamma}^{\lambda}{}_{\alpha \beta} &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \tilde{v}^{\beta} \left(\frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\alpha} \partial \tilde{x}^{\beta}} + \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\beta}} \Gamma^{\sigma}{}_{\mu \nu}\right), \\ \tilde{\Gamma}^{\lambda}{}_{\alpha \beta} &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \left(\frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\alpha} \partial \tilde{x}^{\beta}} + \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\beta}} \Gamma^{\sigma}{}_{\mu \nu}\right) \\ &= \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \frac{\partial x^{\mu}}{\partial \tilde{x}^{\alpha}} \frac{\partial x^{\nu}}{\partial \tilde{x}^{\beta}} \Gamma^{\sigma}{}_{\mu \nu} + \frac{\partial \tilde{x}^{\lambda}}{\partial x^{\sigma}} \frac{\partial^2 x^{\sigma}}{\partial \tilde{x}^{\alpha} \partial \tilde{x}^{\beta}}, \end{align*} ∂ x ~ α ∂ v ~ λ + v ~ ν Γ ~ λ αν v ~ β Γ ~ λ α β Γ ~ λ α β = ∂ x ~ α ∂ x μ ∂ x σ ∂ x ~ λ ( ∂ x μ ∂ v σ + v ν Γ σ μν ) = ∂ x ~ α ∂ x μ ∂ x σ ∂ x ~ λ ( ∂ x μ ∂ ( ∂ x ~ β ∂ x σ v ~ β ) + ∂ x ~ γ ∂ x ν v ~ γ Γ σ μν ) = ∂ x ~ α ∂ x μ ∂ x σ ∂ x ~ λ ( ∂ x μ ∂ x ~ ρ ∂ x ~ ρ ∂ ( ∂ x ~ β ∂ x σ v ~ β ) + ∂ x ~ γ ∂ x ν v ~ γ Γ σ μν ) = ∂ x σ ∂ x ~ λ ( ∂ x ~ α ∂ x μ ∂ x μ ∂ x ~ ρ ( ∂ x ~ ρ ∂ x ~ β ∂ 2 x σ v ~ β + ∂ x ~ β ∂ x σ ∂ x ~ ρ ∂ v ~ β ) + ∂ x ~ α ∂ x μ ∂ x ~ γ ∂ x ν v ~ γ Γ σ μν ) = ∂ x σ ∂ x ~ λ ( δ α ρ ( ∂ x ~ ρ ∂ x ~ β ∂ 2 x σ v ~ β + ∂ x ~ β ∂ x σ ∂ x ~ ρ ∂ v ~ β ) + ∂ x ~ α ∂ x μ ∂ x ~ γ ∂ x ν v ~ γ Γ σ μν ) = ∂ x σ ∂ x ~ λ ( ∂ x ~ α ∂ x ~ β ∂ 2 x σ v ~ β + ∂ x ~ β ∂ x σ ∂ x ~ α ∂ v ~ β + ∂ x ~ α ∂ x μ ∂ x ~ γ ∂ x ν v ~ γ Γ σ μν ) = ∂ x σ ∂ x ~ λ ∂ x ~ α ∂ x ~ β ∂ 2 x σ v ~ β + ∂ x σ ∂ x ~ λ ∂ x ~ β ∂ x σ ∂ x ~ α ∂ v ~ β + ∂ x σ ∂ x ~ λ ∂ x ~ α ∂ x μ ∂ x ~ γ ∂ x ν v ~ γ Γ σ μν = ∂ x σ ∂ x ~ λ ∂ x ~ α ∂ x ~ β ∂ 2 x σ v ~ β + δ β λ ∂ x ~ α ∂ v ~ β + ∂ x σ ∂ x ~ λ ∂ x ~ α ∂ x μ ∂ x ~ γ ∂ x ν v ~ γ Γ σ μν = ∂ x σ ∂ x ~ λ ∂ x ~ α ∂ x ~ β ∂ 2 x σ v ~ β + ∂ x ~ α ∂ v ~ λ + ∂ x σ ∂ x ~ λ ∂ x ~ α ∂ x μ ∂ x ~ β ∂ x ν v ~ β Γ σ μν = ∂ x σ ∂ x ~ λ v ~ β ( ∂ x ~ α ∂ x ~ β ∂ 2 x σ + ∂ x ~ α ∂ x μ ∂ x ~ β ∂ x ν Γ σ μν ) + ∂ x ~ α ∂ v ~ λ , = ∂ x σ ∂ x ~ λ v ~ β ( ∂ x ~ α ∂ x ~ β ∂ 2 x σ + ∂ x ~ α ∂ x μ ∂ x ~ β ∂ x ν Γ σ μν ) , = ∂ x σ ∂ x ~ λ ( ∂ x ~ α ∂ x ~ β ∂ 2 x σ + ∂ x ~ α ∂ x μ ∂ x ~ β ∂ x ν Γ σ μν ) = ∂ x σ ∂ x ~ λ ∂ x ~ α ∂ x μ ∂ x ~ β ∂ x ν Γ σ μν + ∂ x σ ∂ x ~ λ ∂ x ~ α ∂ x ~ β ∂ 2 x σ , we see, that the Christoffel symbols are not tensor.
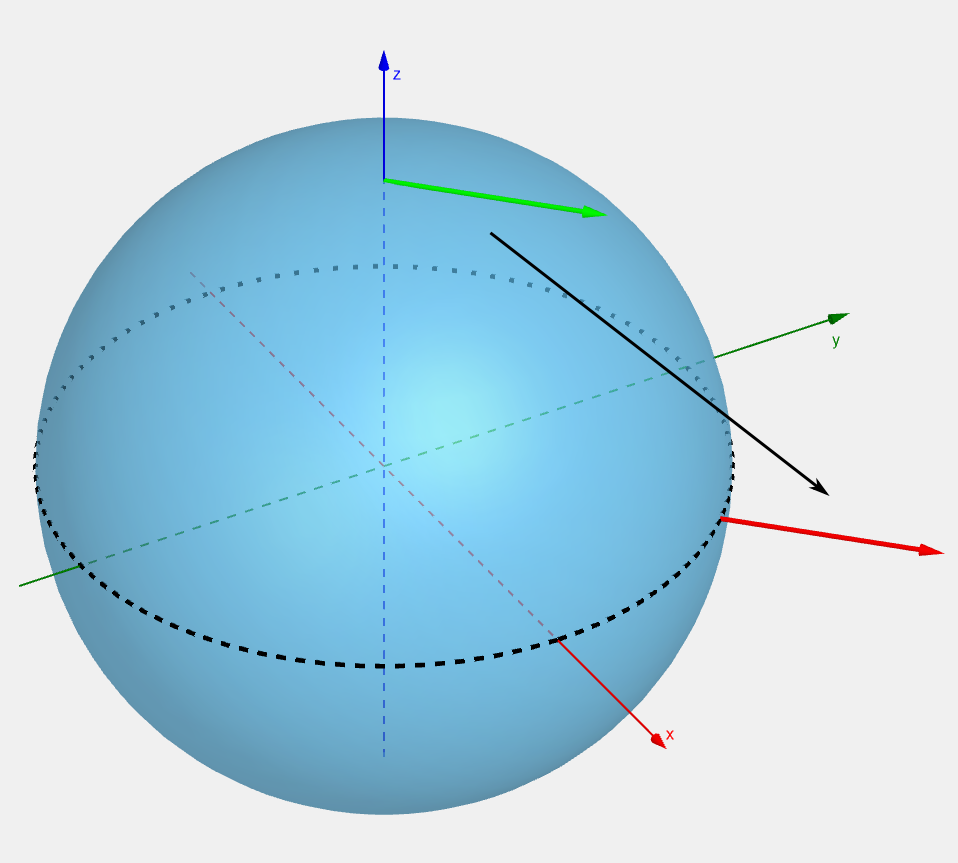
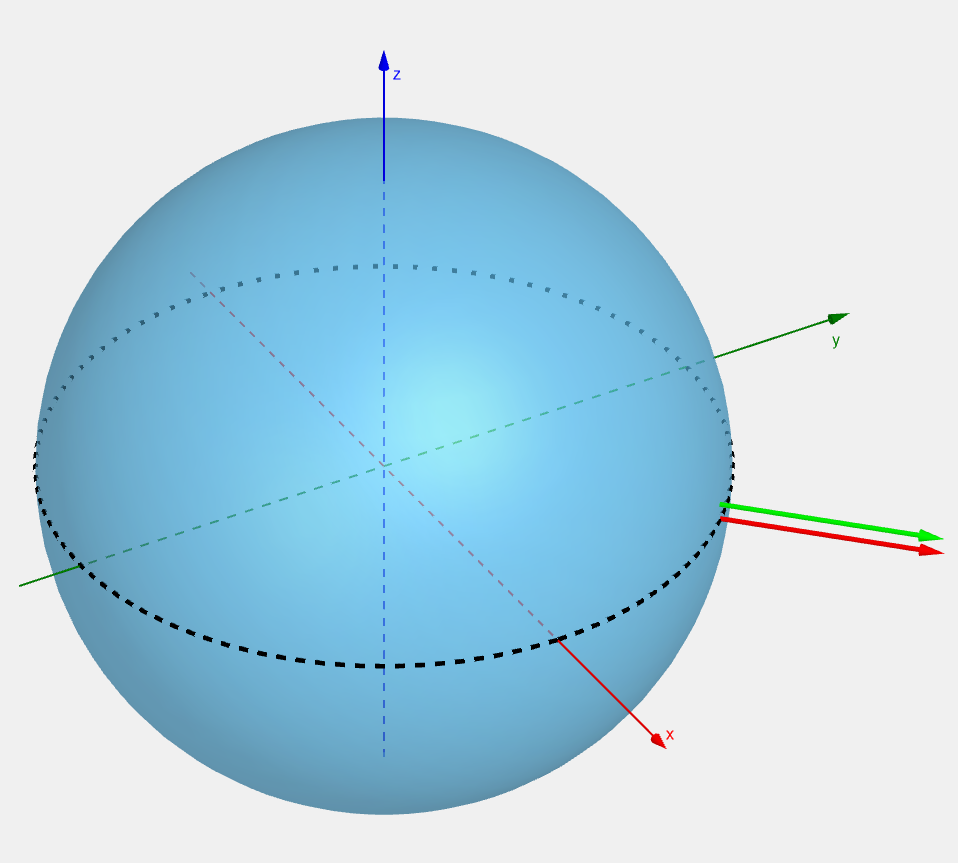
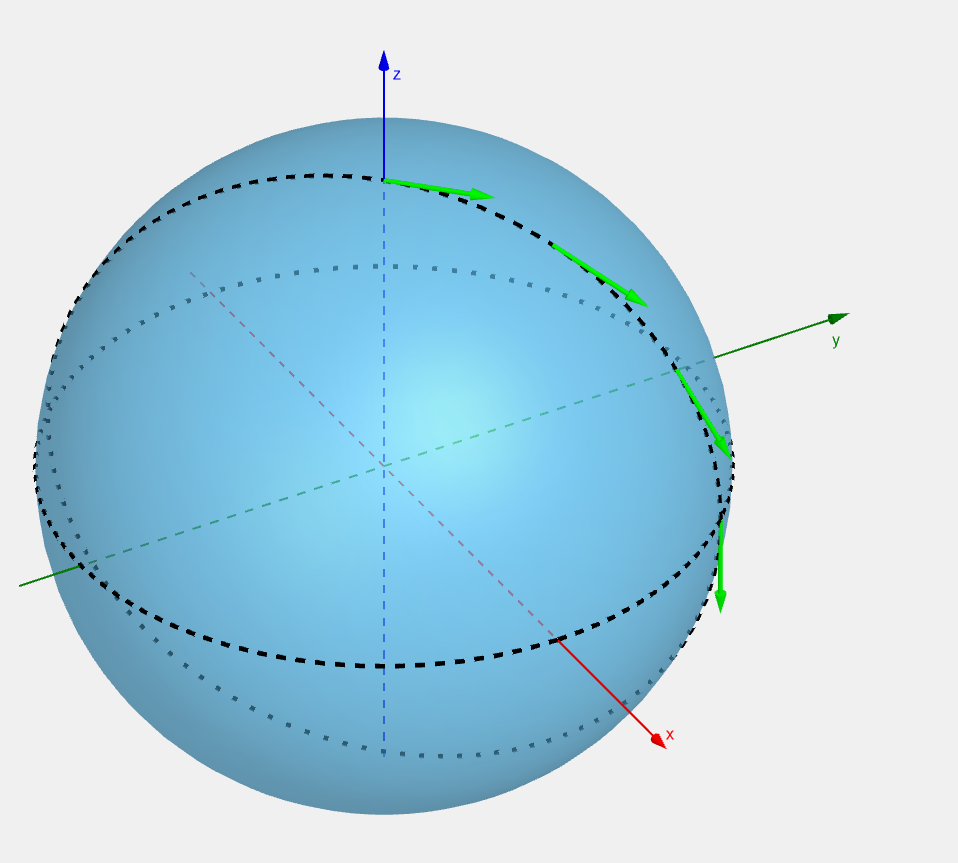
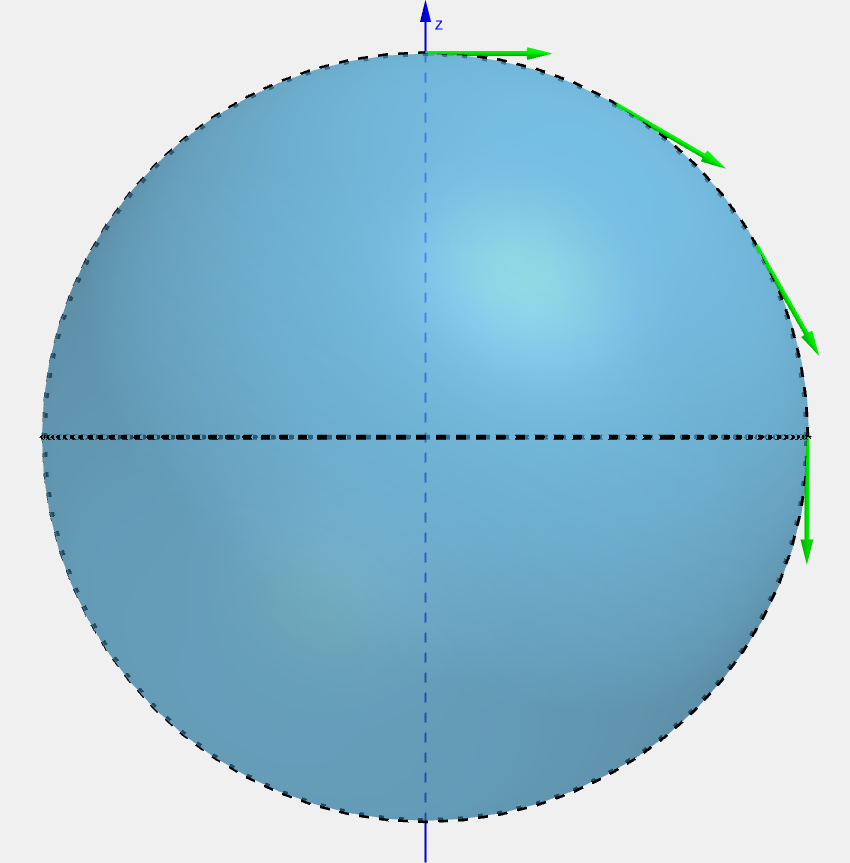
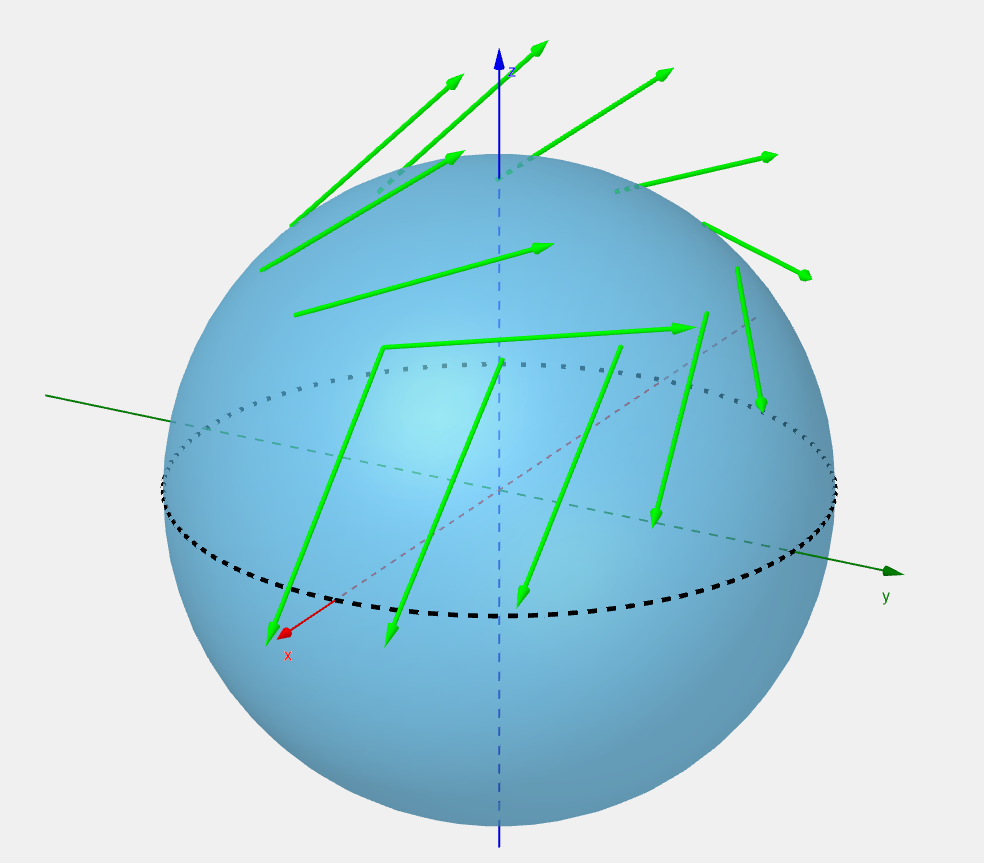
When we want to compare two vectors in flat space, we just slide one over to the other:
And we could naively do this on the surface of the sphere:
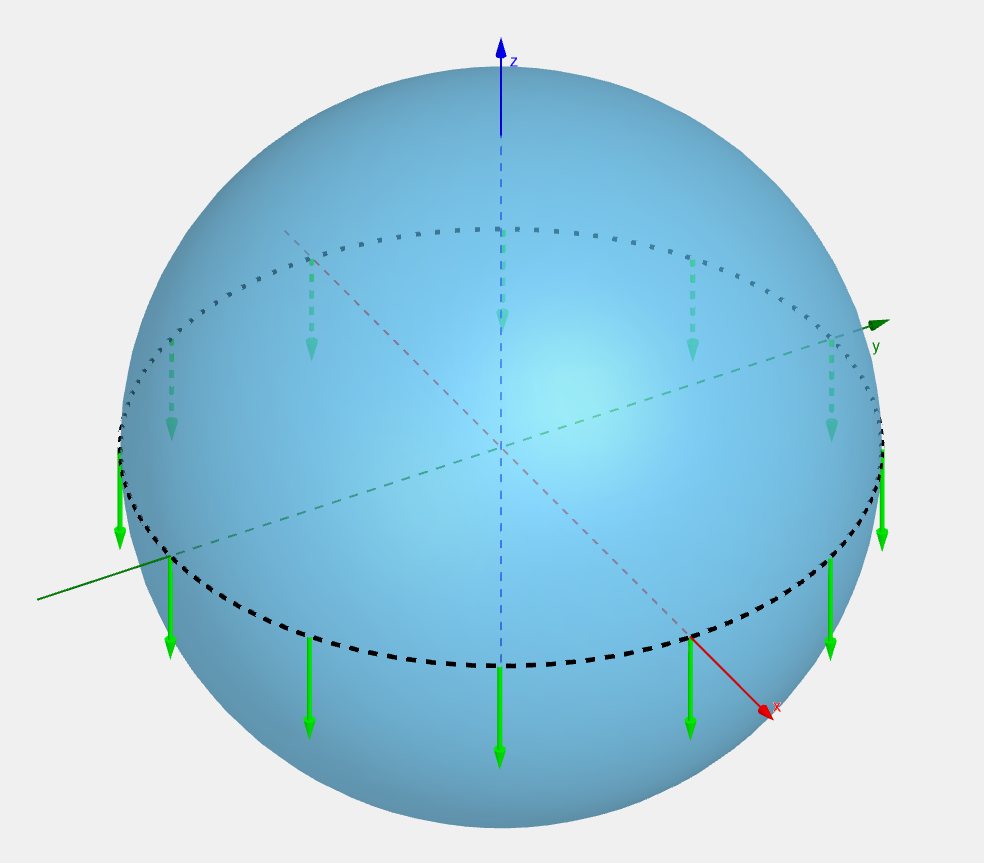
but what we did here is transport it through the higher dimensional (3D) space. If we look at the two vectors from the perspective of someone living on the surface:
we see that they are two different vector. What we need to do is a process called parallel transport:
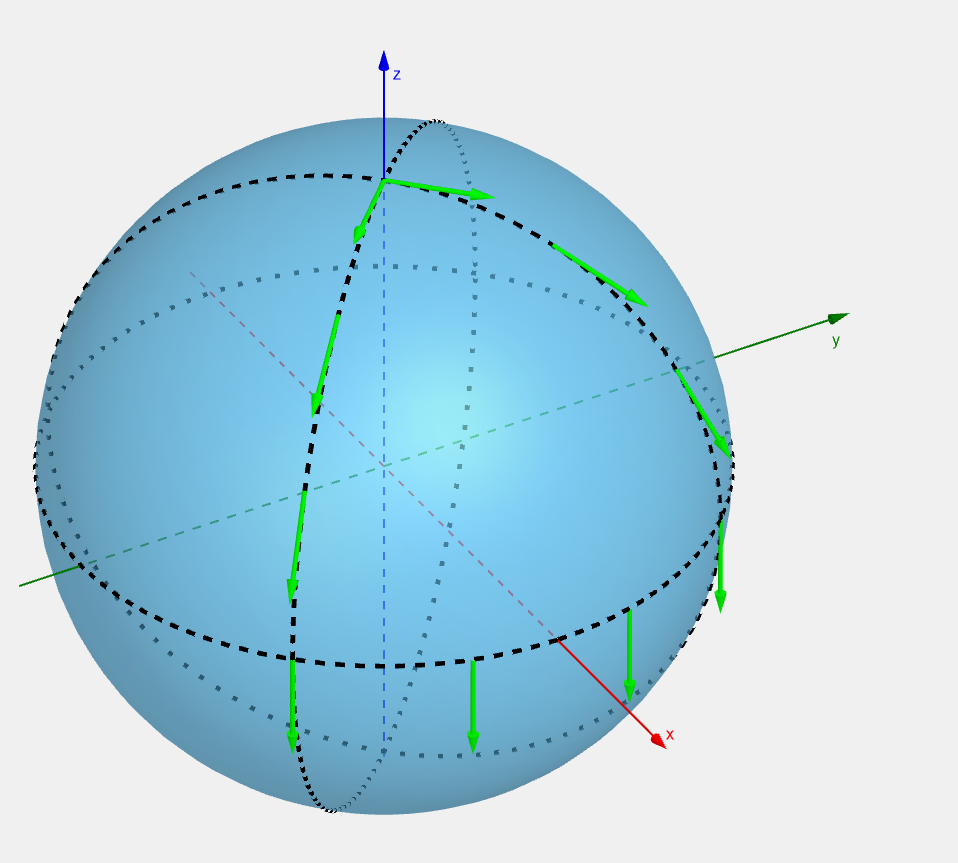
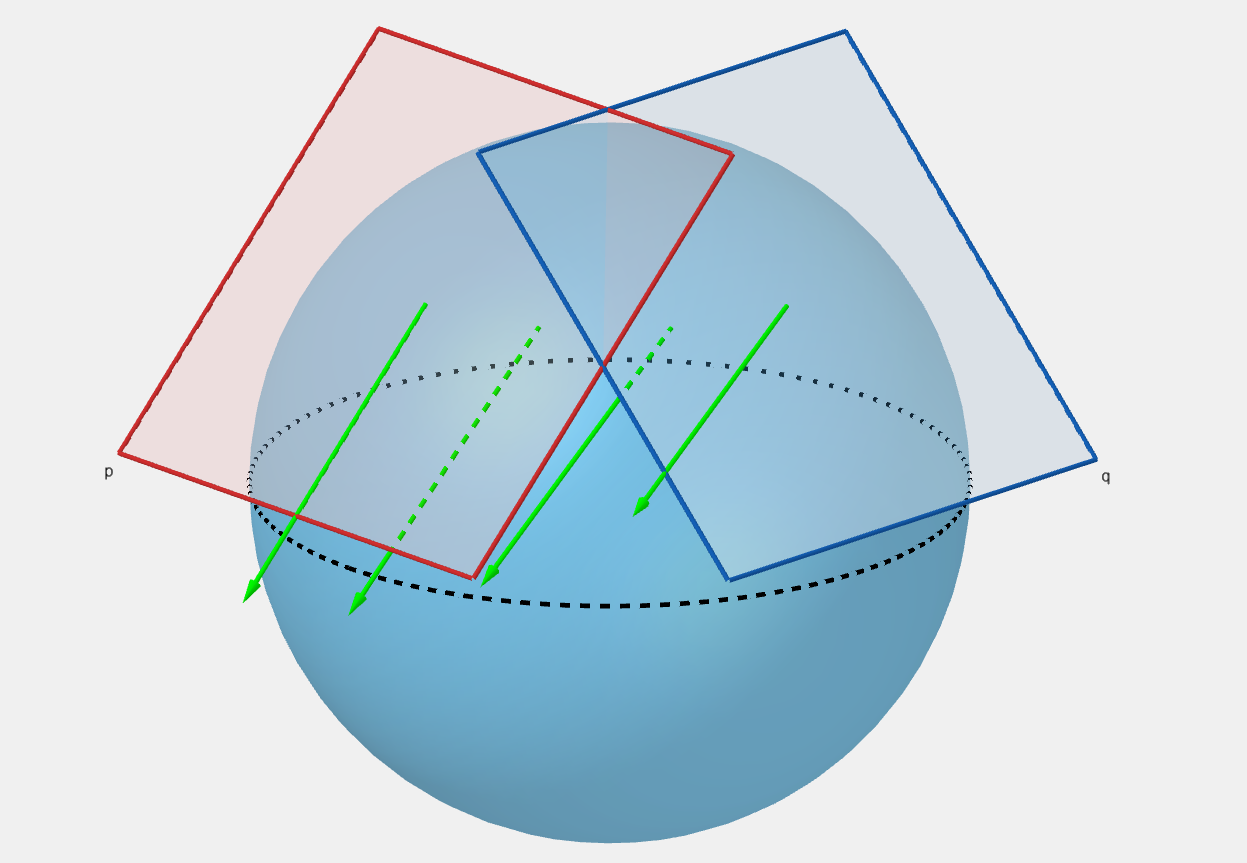
There is a downside to parallel transport. When parallel transporting along a closed curve, the vector may rotate:
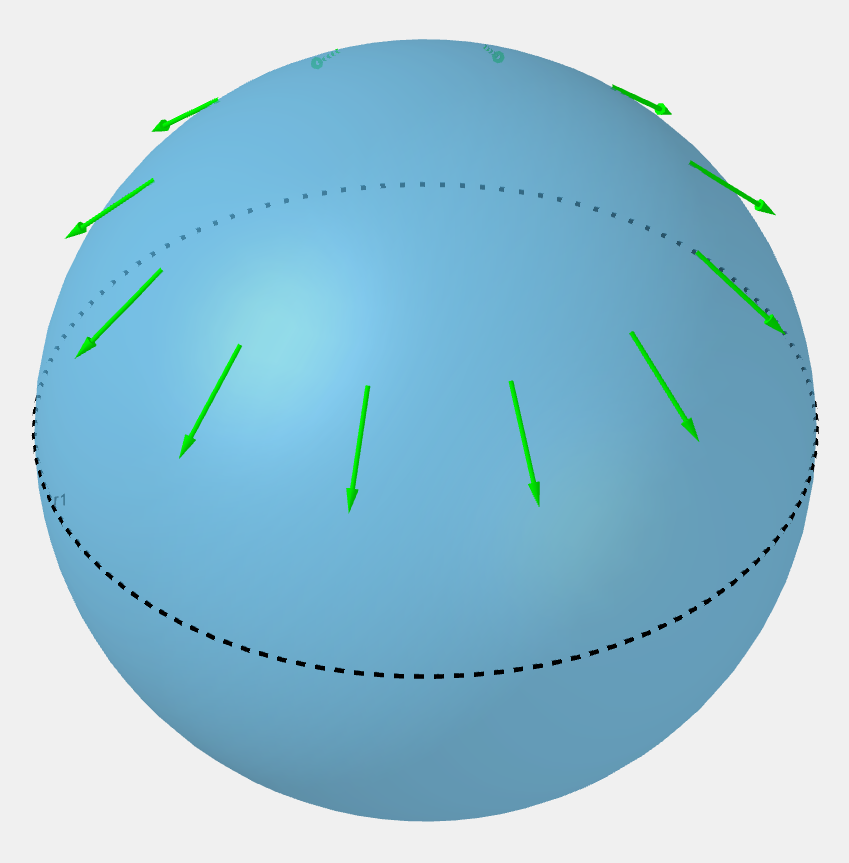
When parallel transporting, the rate of change of the vector is completely in the normal components:
so we may express it as follows when transporting along a path parametrized by λ \lambda λ
d v d λ = n , d v d λ − n = 0 \begin{align*} \frac{d \boldsymbol{v}}{d\lambda} &= \boldsymbol{n}, \\ \frac{d \boldsymbol{v}}{d\lambda} - \boldsymbol{n} &= \boldsymbol{0} \\ \end{align*} d λ d v d λ d v − n = n , = 0 For the extrinsic definition of covariant derivative ∇ w v \nabla_{\boldsymbol{w}} \boldsymbol{v} ∇ w v v \boldsymbol{v} v w \boldsymbol{w} w
∇ d d λ v = d v d λ − n = 0 , \nabla_{\frac{d}{d\lambda}} \boldsymbol{v} = \frac{d\boldsymbol{v}}{d\lambda} - \boldsymbol{n} = \boldsymbol{0}, ∇ d λ d v = d λ d v − n = 0 , so when the covariant derivative is equal to zero, it means that the vector field is parallel transported.
The covariant derivative of tangent vector v \boldsymbol{v} v x μ x^{\mu} x μ
∇ ∂ ∂ x μ v = ∂ v ∂ x μ − n = ∂ ∂ x μ ( v ν e ν ) − n = ∂ v ν ∂ x μ e ν + v ν ∂ e ν ∂ x μ − n = ∂ v ν ∂ x μ e ν + v ν ( Γ σ μ ν e σ + L μ ν n ^ ) − n = ∂ v σ ∂ x μ e σ + v ν Γ σ μ ν e σ + v ν L μ ν n ^ − n = ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) e σ + v ν L μ ν n ^ − n , \begin{align*} \nabla_{\frac{\partial}{\partial x^{\mu}}} \boldsymbol{v} &= \frac{\partial \boldsymbol{v}}{\partial x^{\mu}} - \boldsymbol{n} \\ &= \frac{\partial}{\partial x^{\mu}} \left(v^{\nu} \boldsymbol{e_{\nu}}\right) - \boldsymbol{n} \\ &= \frac{\partial v^{\nu}}{\partial x^{\mu}} \boldsymbol{e_{\nu}} + v^{\nu} \frac{\partial \boldsymbol{e_{\nu}}}{\partial x^{\mu}} - \boldsymbol{n} \\ &= \frac{\partial v^{\nu}}{\partial x^{\mu}} \boldsymbol{e_{\nu}} + v^{\nu} \left(\Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}} + L_{\mu \nu} \boldsymbol{\hat{n}}\right) - \boldsymbol{n} \\ &= \frac{\partial v^{\sigma}}{\partial x^{\mu}} \boldsymbol{e_{\sigma}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}} + v^{\nu} L_{\mu \nu} \boldsymbol{\hat{n}} - \boldsymbol{n} \\ &= \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{e_{\sigma}} + v^{\nu} L_{\mu \nu} \boldsymbol{\hat{n}} - \boldsymbol{n}, \end{align*} ∇ ∂ x μ ∂ v = ∂ x μ ∂ v − n = ∂ x μ ∂ ( v ν e ν ) − n = ∂ x μ ∂ v ν e ν + v ν ∂ x μ ∂ e ν − n = ∂ x μ ∂ v ν e ν + v ν ( Γ σ μν e σ + L μν n ^ ) − n = ∂ x μ ∂ v σ e σ + v ν Γ σ μν e σ + v ν L μν n ^ − n = ( ∂ x μ ∂ v σ + v ν Γ σ μν ) e σ + v ν L μν n ^ − n , since we said we are subtracting the normal components, they cancel:
∇ ∂ ∂ x μ v = ∇ μ v = ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) e σ , \nabla_{\frac{\partial}{\partial x^{\mu}}} \boldsymbol{v} = \nabla_{\mu} \boldsymbol{v} = \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{e_{\sigma}}, ∇ ∂ x μ ∂ v = ∇ μ v = ( ∂ x μ ∂ v σ + v ν Γ σ μν ) e σ , or in component form:
∇ μ v σ = v σ ; μ = ∂ v σ ∂ x μ + v ν Γ σ μ ν , \nabla_{\mu} v^{\sigma} = v^{\sigma}{}_{;\mu} = \frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}, ∇ μ v σ = v σ ; μ = ∂ x μ ∂ v σ + v ν Γ σ μν , and these equations still apply in flat space since we didn't have normal components to begin with.
As an example, consider the intrinsic sphere with coordinates θ \theta θ ϕ \phi ϕ
g μ ν = [ r 2 0 0 r 2 sin 2 θ ] , Γ θ ϕ ϕ = − sin θ cos θ = − 1 2 sin ( 2 θ ) , Γ ϕ θ ϕ = Γ ϕ ϕ θ = cot θ . \begin{align*} g_{\mu \nu} &= \begin{bmatrix} r^2 & 0 \\ 0 & r^2 \sin^2 \theta \end{bmatrix}, \\ \Gamma^{\theta}{}_{\phi \phi} &= -\sin \theta \cos \theta = -\frac{1}{2} \sin (2 \theta), \\ \Gamma^{\phi}{}_{\theta \phi} = \Gamma^{\phi}{}_{\phi \theta} &= \cot \theta. \end{align*} g μν Γ θ ϕϕ Γ ϕ θϕ = Γ ϕ ϕθ = [ r 2 0 0 r 2 sin 2 θ ] , = − sin θ cos θ = − 2 1 sin ( 2 θ ) , = cot θ . And the covariant derivatives of arbitrary vector field v \boldsymbol{v} v
v θ ; θ = ∂ v θ ∂ θ + v ν Γ θ θ ν = ∂ v θ ∂ θ , v θ ; ϕ = ∂ v θ ∂ ϕ + v ν Γ θ ϕ ν = ∂ v θ ∂ ϕ + v ϕ Γ θ ϕ ϕ = ∂ v θ ∂ ϕ − v ϕ 2 sin ( 2 θ ) , v ϕ ; θ = ∂ v ϕ ∂ θ + v ν Γ ϕ θ ν = ∂ v ϕ ∂ θ + v ϕ Γ ϕ θ ϕ = ∂ v ϕ ∂ θ + v ϕ cot θ , v ϕ ; ϕ = ∂ v ϕ ∂ ϕ + v ν Γ ϕ ϕ ν = ∂ v ϕ ∂ ϕ + v θ Γ ϕ ϕ θ = ∂ v ϕ ∂ ϕ + v θ cot θ , \begin{align*} v^{\theta}{}_{;\theta} &= \frac{\partial v^{\theta}}{\partial \theta} + v^{\nu} \Gamma^{\theta}{}_{\theta \nu} \\ &= \frac{\partial v^{\theta}}{\partial \theta}, \\ v^{\theta}{}_{;\phi} &= \frac{\partial v^{\theta}}{\partial \phi} + v^{\nu} \Gamma^{\theta}{}_{\phi \nu} \\ &= \frac{\partial v^{\theta}}{\partial \phi} + v^{\phi} \Gamma^{\theta}{}_{\phi \phi} \\ &= \frac{\partial v^{\theta}}{\partial \phi} - \frac{v^{\phi}}{2} \sin (2\theta), \\ v^{\phi}{}_{;\theta} &= \frac{\partial v^{\phi}}{\partial \theta} + v^{\nu} \Gamma^{\phi}{}_{\theta \nu} \\ &= \frac{\partial v^{\phi}}{\partial \theta} + v^{\phi} \Gamma^{\phi}{}_{\theta \phi} \\ &= \frac{\partial v^{\phi}}{\partial \theta} + v^{\phi} \cot \theta, \\ v^{\phi}{}_{;\phi} &= \frac{\partial v^{\phi}}{\partial \phi} + v^{\nu} \Gamma^{\phi}{}_{\phi \nu} \\ &= \frac{\partial v^{\phi}}{\partial \phi} + v^{\theta} \Gamma^{\phi}{}_{\phi \theta} \\ &= \frac{\partial v^{\phi}}{\partial \phi} + v^{\theta} \cot \theta, \\ \end{align*} v θ ; θ v θ ; ϕ v ϕ ; θ v ϕ ; ϕ = ∂ θ ∂ v θ + v ν Γ θ θ ν = ∂ θ ∂ v θ , = ∂ ϕ ∂ v θ + v ν Γ θ ϕ ν = ∂ ϕ ∂ v θ + v ϕ Γ θ ϕϕ = ∂ ϕ ∂ v θ − 2 v ϕ sin ( 2 θ ) , = ∂ θ ∂ v ϕ + v ν Γ ϕ θ ν = ∂ θ ∂ v ϕ + v ϕ Γ ϕ θϕ = ∂ θ ∂ v ϕ + v ϕ cot θ , = ∂ ϕ ∂ v ϕ + v ν Γ ϕ ϕ ν = ∂ ϕ ∂ v ϕ + v θ Γ ϕ ϕθ = ∂ ϕ ∂ v ϕ + v θ cot θ , cleaning it up:
v θ ; θ = ∂ v θ ∂ θ , v θ ; ϕ = ∂ v θ ∂ ϕ − v ϕ 2 sin ( 2 θ ) , v ϕ ; θ = ∂ v ϕ ∂ θ + v ϕ cot θ , v ϕ ; ϕ = ∂ v ϕ ∂ ϕ + v θ cot θ . \begin{align*} v^{\theta}{}_{;\theta} &= \frac{\partial v^{\theta}}{\partial \theta}, \\ v^{\theta}{}_{;\phi} &= \frac{\partial v^{\theta}}{\partial \phi} - \frac{v^{\phi}}{2} \sin (2\theta), \\ v^{\phi}{}_{;\theta} &= \frac{\partial v^{\phi}}{\partial \theta} + v^{\phi} \cot \theta, \\ v^{\phi}{}_{;\phi} &= \frac{\partial v^{\phi}}{\partial \phi} + v^{\theta} \cot \theta. \end{align*} v θ ; θ v θ ; ϕ v ϕ ; θ v ϕ ; ϕ = ∂ θ ∂ v θ , = ∂ ϕ ∂ v θ − 2 v ϕ sin ( 2 θ ) , = ∂ θ ∂ v ϕ + v ϕ cot θ , = ∂ ϕ ∂ v ϕ + v θ cot θ . Consider the vector field v ( θ , ϕ ) = e θ \boldsymbol{v}(\theta, \phi) = \boldsymbol{e_{\theta}} v ( θ , ϕ ) = e θ θ = π 2 \theta = \frac{\pi}{2} θ = 2 π ϕ = λ \phi = \lambda ϕ = λ
The covariant derivatives are:
v θ ; θ = 0 , v θ ; ϕ = − v ϕ 2 sin ( 2 θ ) , = 0 , v ϕ ; θ = v ϕ cot θ = 0 , v ϕ ; ϕ = v θ cot θ = cot π 2 = 0 , \begin{align*} v^{\theta}{}_{;\theta} &= 0, \\ v^{\theta}{}_{;\phi} &= - \frac{v^{\phi}}{2} \sin (2\theta), \\ &= 0, \\ v^{\phi}{}_{;\theta} &= v^{\phi} \cot \theta \\ &= 0, \\ v^{\phi}{}_{;\phi} &= v^{\theta} \cot \theta \\ &= \cot \frac{\pi}{2} \\ &= 0, \end{align*} v θ ; θ v θ ; ϕ v ϕ ; θ v ϕ ; ϕ = 0 , = − 2 v ϕ sin ( 2 θ ) , = 0 , = v ϕ cot θ = 0 , = v θ cot θ = cot 2 π = 0 , meaning the vector field is a parallel transport of a vector.
We checked if a vector is parallely transported in a vector field. If we want to do the opposite, we specify a vector and curve and demand that the covariant derivative is zero. As an example consider the vector v 0 = e θ \boldsymbol{v_0} = \boldsymbol{e_{\theta}} v 0 = e θ θ = π 4 \theta = \frac{\pi}{4} θ = 4 π ϕ = λ \phi = \lambda ϕ = λ v \boldsymbol{v} v
∇ d d λ v = d v d λ − n = ( d θ d λ ∂ ∂ θ + d ϕ d λ ∂ ∂ ϕ ) v − n = ∂ v ∂ ϕ − n = ∇ ϕ v = 0 , \begin{align*} \nabla_{\frac{d}{d\lambda}} \boldsymbol{v} &= \frac{d \boldsymbol{v}}{d\lambda} - \boldsymbol{n} \\ &= \left(\frac{d \theta}{d \lambda} \frac{\partial}{\partial \theta} + \frac{d \phi}{d \lambda} \frac{\partial}{\partial \phi}\right) \boldsymbol{v} - \boldsymbol{n} \\ &= \frac{\partial \boldsymbol{v}}{\partial \phi} - \boldsymbol{n} \\ &= \nabla_{\phi} \boldsymbol{v} = \boldsymbol{0}, \end{align*} ∇ d λ d v = d λ d v − n = ( d λ d θ ∂ θ ∂ + d λ d ϕ ∂ ϕ ∂ ) v − n = ∂ ϕ ∂ v − n = ∇ ϕ v = 0 , implying:
v θ ; ϕ = 0 , v ϕ ; ϕ = 0. \begin{align*} v^{\theta}{}_{;\phi} &= 0, \\ v^{\phi}{}_{;\phi} &= 0. \end{align*} v θ ; ϕ v ϕ ; ϕ = 0 , = 0. Computing the covariant derivatives:
v θ ; ϕ = ∂ v θ ∂ ϕ − v ϕ 2 sin ( 2 θ ) = ∂ v θ ∂ λ − v ϕ 2 = 0 , v ϕ ; ϕ = ∂ v ϕ ∂ ϕ + v θ cot θ = ∂ v ϕ ∂ λ + v θ = 0. \begin{align*} v^{\theta}{}_{;\phi} &= \frac{\partial v^{\theta}}{\partial \phi} - \frac{v^{\phi}}{2} \sin (2\theta) \\ &= \frac{\partial v^{\theta}}{\partial \lambda} - \frac{v^{\phi}}{2} = 0, \\ v^{\phi}{}_{;\phi} &= \frac{\partial v^{\phi}}{\partial \phi} + v^{\theta} \cot \theta \\ &= \frac{\partial v^{\phi}}{\partial \lambda} + v^{\theta} = 0. \end{align*} v θ ; ϕ v ϕ ; ϕ = ∂ ϕ ∂ v θ − 2 v ϕ sin ( 2 θ ) = ∂ λ ∂ v θ − 2 v ϕ = 0 , = ∂ ϕ ∂ v ϕ + v θ cot θ = ∂ λ ∂ v ϕ + v θ = 0. We have system of partial differential equations describing the vector field:
∂ v θ ∂ λ = v ϕ 2 , ∂ v ϕ ∂ λ = − v θ , \begin{align*} \frac{\partial v^{\theta}}{\partial \lambda} &= \frac{v^{\phi}}{2}, \\ \frac{\partial v^{\phi}}{\partial \lambda} &= -v^{\theta}, \end{align*} ∂ λ ∂ v θ ∂ λ ∂ v ϕ = 2 v ϕ , = − v θ , we can take partial derivative with respect to λ \lambda λ
∂ 2 v θ ∂ λ 2 = 1 2 ∂ v ϕ ∂ λ , ∂ 2 v ϕ ∂ λ 2 = − ∂ v θ ∂ λ , \begin{align*} \frac{\partial^2 v^{\theta}}{\partial \lambda^2} &= \frac{1}{2} \frac{\partial v^{\phi}}{\partial \lambda}, \\ \frac{\partial^2 v^{\phi}}{\partial \lambda^2} &= - \frac{\partial v^{\theta}}{\partial \lambda}, \end{align*} ∂ λ 2 ∂ 2 v θ ∂ λ 2 ∂ 2 v ϕ = 2 1 ∂ λ ∂ v ϕ , = − ∂ λ ∂ v θ , and solve for the first order partial derivatives:
∂ v ϕ ∂ λ = 2 ∂ 2 v θ ∂ λ 2 , ∂ v θ ∂ λ = − ∂ 2 v ϕ ∂ λ 2 , \begin{align*} \frac{\partial v^{\phi}}{\partial \lambda} &= 2 \frac{\partial^2 v^{\theta}}{\partial \lambda^2}, \\ \frac{\partial v^{\theta}}{\partial \lambda} &= -\frac{\partial^2 v^{\phi}}{\partial \lambda^2}, \end{align*} ∂ λ ∂ v ϕ ∂ λ ∂ v θ = 2 ∂ λ 2 ∂ 2 v θ , = − ∂ λ 2 ∂ 2 v ϕ , substituting back:
∂ 2 v θ ∂ λ 2 = − v θ 2 , ∂ 2 v ϕ ∂ λ 2 = − v ϕ 2 . \begin{align*} \frac{\partial^2 v^{\theta}}{\partial \lambda^2} &= -\frac{v^{\theta}}{2}, \\ \frac{\partial^2 v^{\phi}}{\partial \lambda^2} &= -\frac{v^{\phi}}{2}. \end{align*} ∂ λ 2 ∂ 2 v θ ∂ λ 2 ∂ 2 v ϕ = − 2 v θ , = − 2 v ϕ . The solution to these equations are:
v θ = A sin λ 2 + B cos λ 2 , v ϕ = C sin λ 2 + D cos λ 2 . \begin{align*} v^{\theta} &= A \sin \frac{\lambda}{\sqrt{2}} + B \cos \frac{\lambda}{\sqrt{2}}, \\ v^{\phi} &= C \sin \frac{\lambda}{\sqrt{2}} + D \cos \frac{\lambda}{\sqrt{2}}. \end{align*} v θ v ϕ = A sin 2 λ + B cos 2 λ , = C sin 2 λ + D cos 2 λ . When we substitute λ = 0 \lambda = 0 λ = 0 v = v 0 = e θ \boldsymbol{v} = \boldsymbol{v_0} = \boldsymbol{e_{\theta}} v = v 0 = e θ
v θ = B = 1 , v ϕ = D = 0 , \begin{align*} v^{\theta} &= B = 1, \\ v^{\phi} &= D = 0, \end{align*} v θ v ϕ = B = 1 , = D = 0 , implying:
v θ = A sin λ 2 + cos λ 2 , v ϕ = C sin λ 2 . \begin{align*} v^{\theta} &= A \sin \frac{\lambda}{\sqrt{2}} + \cos \frac{\lambda}{\sqrt{2}}, \\ v^{\phi} &= C \sin \frac{\lambda}{\sqrt{2}}. \end{align*} v θ v ϕ = A sin 2 λ + cos 2 λ , = C sin 2 λ . The derivatives are equal to:
∂ v θ ∂ λ = A 2 cos λ 2 − 1 2 sin λ 2 , ∂ v ϕ ∂ λ = C 2 cos λ 2 . \begin{align*} \frac{\partial v^{\theta}}{\partial \lambda} &= \frac{A}{\sqrt{2}} \cos \frac{\lambda}{\sqrt{2}} - \frac{1}{\sqrt{2}} \sin \frac{\lambda}{\sqrt{2}}, \\ \frac{\partial v^{\phi}}{\partial \lambda} &= \frac{C}{\sqrt{2}} \cos \frac{\lambda}{\sqrt{2}}. \end{align*} ∂ λ ∂ v θ ∂ λ ∂ v ϕ = 2 A cos 2 λ − 2 1 sin 2 λ , = 2 C cos 2 λ . We already have formula for the derivatives:
∂ v θ ∂ λ = v ϕ 2 = C 2 sin λ 2 , ∂ v ϕ ∂ λ = − v θ = − ( A sin λ 2 + cos λ 2 ) , \begin{align*} \frac{\partial v^{\theta}}{\partial \lambda} &= \frac{v^{\phi}}{2} = \frac{C}{2} \sin \frac{\lambda}{\sqrt{2}}, \\ \frac{\partial v^{\phi}}{\partial \lambda} &= -v^{\theta} = -(A \sin \frac{\lambda}{\sqrt{2}} + \cos \frac{\lambda}{\sqrt{2}}), \end{align*} ∂ λ ∂ v θ ∂ λ ∂ v ϕ = 2 v ϕ = 2 C sin 2 λ , = − v θ = − ( A sin 2 λ + cos 2 λ ) , and substituting v θ v^{\theta} v θ v ϕ v^{\phi} v ϕ
A 2 cos λ 2 − 1 2 sin λ 2 = C 2 sin λ 2 , C 2 cos λ 2 = − ( A sin λ 2 + cos λ 2 ) . \begin{align*} \frac{A}{\sqrt{2}} \cos \frac{\lambda}{\sqrt{2}} - \frac{1}{\sqrt{2}} \sin \frac{\lambda}{\sqrt{2}} &= \frac{C}{2} \sin \frac{\lambda}{\sqrt{2}}, \\ \frac{C}{\sqrt{2}} \cos \frac{\lambda}{\sqrt{2}} &= -(A \sin \frac{\lambda}{\sqrt{2}} + \cos \frac{\lambda}{\sqrt{2}}). \end{align*} 2 A cos 2 λ − 2 1 sin 2 λ 2 C cos 2 λ = 2 C sin 2 λ , = − ( A sin 2 λ + cos 2 λ ) . We can substitute λ = 0 \lambda = 0 λ = 0
A 2 = 0 , C 2 = − 1 , \begin{align*} \frac{A}{\sqrt{2}} &= 0, \\ \frac{C}{\sqrt{2}} &= -1, \end{align*} 2 A 2 C = 0 , = − 1 , and solve for the constants:
A = 0 , C = − 2 . \begin{align*} A &= 0, \\ C &= -\sqrt{2}. \end{align*} A C = 0 , = − 2 . So the equations are as follows:
v θ = cos λ 2 , v ϕ = − 2 sin λ 2 , \begin{align*} v^{\theta} &= \cos \frac{\lambda}{\sqrt{2}}, \\ v^{\phi} &= -\sqrt{2} \sin \frac{\lambda}{\sqrt{2}}, \end{align*} v θ v ϕ = cos 2 λ , = − 2 sin 2 λ , and the vector field:
v ( θ , ϕ ) = cos λ 2 e θ − 2 sin λ 2 e ϕ . \boldsymbol{v}(\theta, \phi) = \cos \frac{\lambda}{\sqrt{2}} \boldsymbol{e_{\theta}} - \sqrt{2} \sin \frac{\lambda}{\sqrt{2}} \boldsymbol{e_{\phi}}. v ( θ , ϕ ) = cos 2 λ e θ − 2 sin 2 λ e ϕ . The squared length of the initial vector v 0 \boldsymbol{v_0} v 0
∣ v 0 ∣ 2 = g μ ν v 0 μ v 0 ν = r 2 . \begin{align*} |\boldsymbol{v_0}|^2 &= g_{\mu \nu} v_0^{\mu} v_0^{\nu} \\ &= r^2. \end{align*} ∣ v 0 ∣ 2 = g μν v 0 μ v 0 ν = r 2 . And for the vector field v \boldsymbol{v} v
∣ v ∣ 2 = g μ ν v μ v ν = ( cos λ 2 ) 2 r 2 + ( − 2 sin λ 2 ) 2 r 2 sin 2 θ = r 2 ( cos 2 λ 2 r 2 + 2 sin 2 λ 2 sin 2 π 4 ) 2 = r 2 ( cos 2 λ 2 r 2 + sin 2 λ 2 ) 2 = r 2 , \begin{align*} |\boldsymbol{v}|^2 &= g_{\mu \nu} v^{\mu} v^{\nu} \\ &= \left(\cos \frac{\lambda}{\sqrt{2}}\right)^2 r^2 + \left(-\sqrt{2} \sin \frac{\lambda}{\sqrt{2}}\right)^2 r^2 \sin^2 \theta \\ &= r^2 \left(\cos^2 \frac{\lambda}{\sqrt{2}} r^2 + 2 \sin^2 \frac{\lambda}{\sqrt{2}} \sin^2 \frac{\pi}{4}\right)^2 \\ &= r^2 \left(\cos^2 \frac{\lambda}{\sqrt{2}} r^2 + \sin^2 \frac{\lambda}{\sqrt{2}}\right)^2 \\ &= r^2, \end{align*} ∣ v ∣ 2 = g μν v μ v ν = ( cos 2 λ ) 2 r 2 + ( − 2 sin 2 λ ) 2 r 2 sin 2 θ = r 2 ( cos 2 2 λ r 2 + 2 sin 2 2 λ sin 2 4 π ) 2 = r 2 ( cos 2 2 λ r 2 + sin 2 2 λ ) 2 = r 2 , Keeping the vector length constant.
In intrinsic geometry, the covariant derivative is the same:
∇ ∂ ∂ x μ v = ∇ μ v = ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) e σ , ∇ μ v σ = v σ ; μ = ∂ v σ ∂ x μ + v ν Γ σ μ ν , \begin{align*} \nabla_{\frac{\partial}{\partial x^{\mu}}} \boldsymbol{v} &= \nabla_{\mu} \boldsymbol{v} = \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{e_{\sigma}}, \\ \nabla_{\mu} v^{\sigma} = v^{\sigma}{}_{;\mu} &= \frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}, \end{align*} ∇ ∂ x μ ∂ v ∇ μ v σ = v σ ; μ = ∇ μ v = ( ∂ x μ ∂ v σ + v ν Γ σ μν ) e σ , = ∂ x μ ∂ v σ + v ν Γ σ μν , and setting covariant derivative equal to zero still means it is parallel transported. However the following definition of the Christoffel symbols does not work, because we had to consider the extrinsic space for the dot product:
Γ μ ν λ = ∂ e μ ∂ x ν ⋅ e σ g σ λ . \Gamma^{\lambda}_{\mu \nu} = \frac{\partial \boldsymbol{e_{\mu}}}{\partial x^{\nu}} \cdot \boldsymbol{e_{\sigma}} g^{\sigma \lambda}. Γ μν λ = ∂ x ν ∂ e μ ⋅ e σ g σλ . We also had to consider the extrinsic geometry for the metric tensor. There is however nothing we can do about this and the metric tensor has to be defined, obtained from an equation or obtained using from an extrinsic space. We can think of the case of the Cartesian metric tensor - the metric tensor is defined for us and there is no way to derive it.
When working with intrinsic geometry, we also cannot use the extrinsic position vector R \boldsymbol{R} R
e μ = ∂ R ∂ x μ , \boldsymbol{e_{\mu}} = \frac{\partial \boldsymbol{R}}{\partial x^{\mu}}, e μ = ∂ x μ ∂ R , we write it like this:
e μ = ∂ ∂ x μ . \boldsymbol{e_{\mu}} = \frac{\partial}{\partial x^{\mu}}. e μ = ∂ x μ ∂ . In extrinsic geometry, we started by defining the covariant derivative as the derivative with the normal components subtracted:
∇ d d λ v = d v d λ − n . \nabla_{\frac{d}{d\lambda}} \boldsymbol{v} = \frac{d\boldsymbol{v}}{d\lambda} - \boldsymbol{n}. ∇ d λ d v = d λ d v − n . But when considering the intrinsic geometry, we do not have a normal components
∇ d d λ v = d v d λ . \nabla_{\frac{d}{d\lambda}} \boldsymbol{v} = \frac{d\boldsymbol{v}}{d\lambda}. ∇ d λ d v = d λ d v . Consider the covariant derivative in the direction of x μ x^{\mu} x μ
∇ ∂ ∂ x μ v = ∂ v ∂ x μ = ∂ ∂ x μ ( v ν e ν ) = ∂ v ν ∂ x μ e ν + v ν ∂ e ν ∂ x μ = ∂ v ν ∂ x μ e ν + v ν ( Γ μ ν σ e σ + L μ ν n ^ ) = ∂ v σ ∂ x μ e σ + v ν Γ μ ν σ e σ + v ν L μ ν n ^ = ( ∂ v σ ∂ x μ + v ν Γ μ ν σ ) e σ + v ν L μ ν n ^ , \begin{align*} \nabla_{\frac{\partial}{\partial x^{\mu}}} \boldsymbol{v} &= \frac{\partial \boldsymbol{v}}{\partial x^{\mu}} \\ &= \frac{\partial}{\partial x^{\mu}} \left(v^{\nu} \boldsymbol{e_{\nu}}\right) \\ &= \frac{\partial v^{\nu}}{\partial x^{\mu}} \boldsymbol{e_{\nu}} + v^{\nu} \frac{\partial \boldsymbol{e_{\nu}}}{\partial x^{\mu}} \\ &= \frac{\partial v^{\nu}}{\partial x^{\mu}} \boldsymbol{e_{\nu}} + v^{\nu} \left(\Gamma^{\sigma}_{\mu \nu} \boldsymbol{e_{\sigma}} + L_{\mu \nu} \boldsymbol{\hat{n}}\right) \\ &= \frac{\partial v^{\sigma}}{\partial x^{\mu}} \boldsymbol{e_{\sigma}} + v^{\nu} \Gamma^{\sigma}_{\mu \nu} \boldsymbol{e_{\sigma}} + v^{\nu} L_{\mu \nu} \boldsymbol{\hat{n}} \\ &= \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}_{\mu \nu}\right) \boldsymbol{e_{\sigma}} + v^{\nu} L_{\mu \nu} \boldsymbol{\hat{n}}, \end{align*} ∇ ∂ x μ ∂ v = ∂ x μ ∂ v = ∂ x μ ∂ ( v ν e ν ) = ∂ x μ ∂ v ν e ν + v ν ∂ x μ ∂ e ν = ∂ x μ ∂ v ν e ν + v ν ( Γ μν σ e σ + L μν n ^ ) = ∂ x μ ∂ v σ e σ + v ν Γ μν σ e σ + v ν L μν n ^ = ( ∂ x μ ∂ v σ + v ν Γ μν σ ) e σ + v ν L μν n ^ , and again, since the normal components don't exist, we can ignore them:
∇ ∂ ∂ x μ v = ( ∂ v σ ∂ x μ + v ν Γ μ ν σ ) e σ , \nabla_{\frac{\partial}{\partial x^{\mu}}} \boldsymbol{v} = \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}_{\mu \nu}\right) \boldsymbol{e_{\sigma}}, ∇ ∂ x μ ∂ v = ( ∂ x μ ∂ v σ + v ν Γ μν σ ) e σ , or in coponent form:
∇ μ v σ = v σ ; μ = ∂ v σ ∂ x μ + v ν Γ μ ν σ , \nabla_{\mu} v^{\sigma} = v^{\sigma}{}_{;\mu} = \frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}_{\mu \nu}, ∇ μ v σ = v σ ; μ = ∂ x μ ∂ v σ + v ν Γ μν σ , and these equations also work in extrinsic geometry.
Recall the following properties:
g μ ν = g ν μ , Γ λ μ ν = Γ λ ν μ . \begin{align*} g_{\mu \nu} &= g_{\nu \mu}, \\ \Gamma^{\lambda}{}_{\mu \nu} &= \Gamma^{\lambda}{}_{\nu \mu}. \end{align*} g μν Γ λ μν = g νμ , = Γ λ νμ . If we take derivative of metric tensor component with respect to a coordinate, we get:
g μ ν , σ = ∂ g μ ν ∂ x σ = ∂ ∂ x σ ( e μ ⋅ e ν ) = ∂ e μ ∂ x σ ⋅ e ν + e μ ⋅ ∂ e ν ∂ x σ = Γ λ μ σ e λ ⋅ e ν + Γ λ ν σ e μ ⋅ e λ , g μ ν , σ = Γ λ μ σ g λ ν + Γ λ ν σ g μ λ . \begin{align*} g_{\mu \nu, \sigma} = \frac{\partial g_{\mu \nu}}{\partial x^{\sigma}} &= \frac{\partial}{\partial x^{\sigma}} (\boldsymbol{e_{\mu}} \cdot \boldsymbol{e_{\nu}}) \\ &= \frac{\partial \boldsymbol{e_{\mu}}}{\partial x^{\sigma}} \cdot \boldsymbol{e_{\nu}} + \boldsymbol{e_{\mu}} \cdot \frac{\partial \boldsymbol{e_{\nu}}}{\partial x^{\sigma}} \\ &= \Gamma^{\lambda}{}_{\mu \sigma} \boldsymbol{e_{\lambda}} \cdot \boldsymbol{e_{\nu}} + \Gamma^{\lambda}{}_{\nu \sigma} \boldsymbol{e_{\mu}} \cdot \boldsymbol{e_{\lambda}}, \\ g_{\mu \nu, \sigma} &= \Gamma^{\lambda}{}_{\mu \sigma} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\nu \sigma} g_{\mu \lambda}. \\ \end{align*} g μν , σ = ∂ x σ ∂ g μν g μν , σ = ∂ x σ ∂ ( e μ ⋅ e ν ) = ∂ x σ ∂ e μ ⋅ e ν + e μ ⋅ ∂ x σ ∂ e ν = Γ λ μ σ e λ ⋅ e ν + Γ λ ν σ e μ ⋅ e λ , = Γ λ μ σ g λ ν + Γ λ ν σ g μ λ . If we swap ν \nu ν σ \sigma σ
g μ σ , ν = Γ λ μ ν g λ σ + Γ λ σ ν g μ λ = Γ λ μ ν g λ σ + Γ λ ν σ g μ λ , \begin{align*} g_{\mu \sigma, \nu} &= \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \sigma} + \Gamma^{\lambda}{}_{\sigma \nu} g_{\mu \lambda} \\ &= \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \sigma} + \Gamma^{\lambda}{}_{\nu \sigma} g_{\mu \lambda}, \end{align*} g μ σ , ν = Γ λ μν g λσ + Γ λ σ ν g μ λ = Γ λ μν g λσ + Γ λ ν σ g μ λ , and if we swap μ \mu μ σ \sigma σ
g σ ν , μ = Γ λ σ μ g λ ν + Γ λ ν μ g σ λ = Γ λ μ σ g λ ν + Γ λ μ ν g λ σ . \begin{align*} g_{\sigma \nu, \mu} &= \Gamma^{\lambda}{}_{\sigma \mu} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\nu \mu} g_{\sigma \lambda} \\ &= \Gamma^{\lambda}{}_{\mu \sigma} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \sigma}. \end{align*} g σ ν , μ = Γ λ σ μ g λ ν + Γ λ νμ g σλ = Γ λ μ σ g λ ν + Γ λ μν g λσ . There are some similar components, if we add g μ ν , σ g_{\mu \nu, \sigma} g μν , σ g μ σ , ν g_{\mu \sigma, \nu} g μ σ , ν
g μ ν , σ + g μ σ , ν = Γ λ μ σ g λ ν + Γ λ ν σ g μ λ + Γ λ μ ν g λ σ + Γ λ ν σ g μ λ = Γ λ μ σ g λ ν + Γ λ μ ν g λ σ + 2 Γ λ ν σ g μ λ , \begin{align*} g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} &= \Gamma^{\lambda}{}_{\mu \sigma} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\nu \sigma} g_{\mu \lambda} + \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \sigma} + \Gamma^{\lambda}{}_{\nu \sigma} g_{\mu \lambda} \\ &= \Gamma^{\lambda}{}_{\mu \sigma} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \sigma} + 2\Gamma^{\lambda}{}_{\nu \sigma} g_{\mu \lambda}, \end{align*} g μν , σ + g μ σ , ν = Γ λ μ σ g λ ν + Γ λ ν σ g μ λ + Γ λ μν g λσ + Γ λ ν σ g μ λ = Γ λ μ σ g λ ν + Γ λ μν g λσ + 2 Γ λ ν σ g μ λ , and subtract g σ ν , μ g_{\sigma \nu, \mu} g σ ν , μ
g μ ν , σ + g μ σ , ν − g σ ν , μ = Γ λ μ σ g λ ν + Γ λ μ ν g λ σ + 2 Γ λ ν σ g μ λ − ( Γ λ μ σ g λ ν + Γ λ μ ν g λ σ ) = 2 Γ λ ν σ g μ λ , Γ λ ν σ g μ λ = 1 2 ( g μ ν , σ + g μ σ , ν − g σ ν , μ ) , Γ λ ν σ g μ λ g μ ρ = 1 2 ( g μ ν , σ + g μ σ , ν − g σ ν , μ ) , Γ λ ν σ δ λ ρ = 1 2 g μ ρ ( g μ ν , σ + g μ σ , ν − g σ ν , μ ) , Γ ρ ν σ = 1 2 g μ ρ ( g μ ν , σ + g μ σ , ν − g σ ν , μ ) = 1 2 g μ ρ ( ∂ g μ ν ∂ x σ + ∂ g μ σ ∂ x ν − ∂ g σ ν ∂ x μ ) , \begin{align*} g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} - g_{\sigma \nu, \mu} &= \Gamma^{\lambda}{}_{\mu \sigma} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \sigma} + 2\Gamma^{\lambda}{}_{\nu \sigma} g_{\mu \lambda} - ( \Gamma^{\lambda}{}_{\mu \sigma} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \sigma}) \\ &= 2\Gamma^{\lambda}{}_{\nu \sigma} g_{\mu \lambda}, \\ \Gamma^{\lambda}{}_{\nu \sigma} g_{\mu \lambda} &= \frac{1}{2} (g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} - g_{\sigma \nu, \mu}), \\ \Gamma^{\lambda}{}_{\nu \sigma} g_{\mu \lambda} g^{\mu \rho} &= \frac{1}{2} (g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} - g_{\sigma \nu, \mu}), \\ \Gamma^{\lambda}{}_{\nu \sigma} \delta_{\lambda}^{\rho} &= \frac{1}{2} g^{\mu \rho} (g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} - g_{\sigma \nu, \mu}), \\ \Gamma^{\rho}{}_{\nu \sigma} &= \frac{1}{2} g^{\mu \rho} (g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} - g_{\sigma \nu, \mu}) \\ &= \frac{1}{2} g^{\mu \rho} \left(\frac{\partial g_{\mu \nu}}{\partial x^{\sigma}} + \frac{\partial g_{\mu \sigma}}{\partial x^{\nu}} - \frac{\partial g_{\sigma \nu}}{\partial x^{\mu}}\right), \end{align*} g μν , σ + g μ σ , ν − g σ ν , μ Γ λ ν σ g μ λ Γ λ ν σ g μ λ g μ ρ Γ λ ν σ δ λ ρ Γ ρ ν σ = Γ λ μ σ g λ ν + Γ λ μν g λσ + 2 Γ λ ν σ g μ λ − ( Γ λ μ σ g λ ν + Γ λ μν g λσ ) = 2 Γ λ ν σ g μ λ , = 2 1 ( g μν , σ + g μ σ , ν − g σ ν , μ ) , = 2 1 ( g μν , σ + g μ σ , ν − g σ ν , μ ) , = 2 1 g μ ρ ( g μν , σ + g μ σ , ν − g σ ν , μ ) , = 2 1 g μ ρ ( g μν , σ + g μ σ , ν − g σ ν , μ ) = 2 1 g μ ρ ( ∂ x σ ∂ g μν + ∂ x ν ∂ g μ σ − ∂ x μ ∂ g σ ν ) , we have arrived at the equation for Christoffel symbols in intrinsic geometry. This formula also works in extrinsic geometry.
If we take the covariant derivative of vector along itself, we get:
∇ d d λ d d λ = d d λ ( d d λ ) = d d λ ( d x μ d λ ∂ ∂ x μ ) = d 2 x μ d λ 2 e μ + d x μ d λ d e μ d λ = d 2 x μ d λ 2 e μ + d x μ d λ d x ν d λ ∂ e μ ∂ x ν = d 2 x σ d λ 2 e σ + d x μ d λ d x ν d λ Γ μ ν σ e σ = ( d 2 x σ d λ 2 + d x μ d λ d x ν d λ Γ μ ν σ ) e σ \begin{align*} \nabla_{\frac{d}{d\lambda}} \frac{d}{d\lambda} &= \frac{d}{d\lambda} \left(\frac{d}{d\lambda}\right) \\ &= \frac{d}{d\lambda} \left(\frac{d x^{\mu}}{d \lambda} \frac{\partial}{\partial x^{\mu}}\right) \\ &= \frac{d^2 x^{\mu}}{d \lambda^2} \boldsymbol{e_{\mu}} + \frac{d x^{\mu}}{d \lambda} \frac{d \boldsymbol{e_{\mu}}}{d \lambda} \\ &= \frac{d^2 x^{\mu}}{d \lambda^2} \boldsymbol{e_{\mu}} + \frac{d x^{\mu}}{d \lambda} \frac{d x^{\nu}}{d \lambda} \frac{\partial \boldsymbol{e_{\mu}}}{\partial x^{\nu}} \\ &= \frac{d^2 x^{\sigma}}{d \lambda^2} \boldsymbol{e_{\sigma}} + \frac{d x^{\mu}}{d \lambda} \frac{d x^{\nu}}{d \lambda} \Gamma^{\sigma}_{\mu \nu} \boldsymbol{e_{\sigma}} \\ &= \left(\frac{d^2 x^{\sigma}}{d \lambda^2} + \frac{d x^{\mu}}{d \lambda} \frac{d x^{\nu}}{d \lambda} \Gamma^{\sigma}_{\mu \nu}\right) \boldsymbol{e_{\sigma}} \end{align*} ∇ d λ d d λ d = d λ d ( d λ d ) = d λ d ( d λ d x μ ∂ x μ ∂ ) = d λ 2 d 2 x μ e μ + d λ d x μ d λ d e μ = d λ 2 d 2 x μ e μ + d λ d x μ d λ d x ν ∂ x ν ∂ e μ = d λ 2 d 2 x σ e σ + d λ d x μ d λ d x ν Γ μν σ e σ = ( d λ 2 d 2 x σ + d λ d x μ d λ d x ν Γ μν σ ) e σ and in the geodesics chapter , we have already seen that this is the tangential acceleration. And if we set this equal to zero, we have the geodesic equations:
d 2 x σ d λ 2 + d x μ d λ d x ν d λ Γ μ ν σ = 0. \frac{d^2 x^{\sigma}}{d \lambda^2} + \frac{d x^{\mu}}{d \lambda} \frac{d x^{\nu}}{d \lambda} \Gamma^{\sigma}_{\mu \nu} = 0. d λ 2 d 2 x σ + d λ d x μ d λ d x ν Γ μν σ = 0. Or, this can be rewritten for a vector v \boldsymbol{v} v
∇ v v = 0 , \nabla_{\boldsymbol{v}} \boldsymbol{v} = \boldsymbol{0}, ∇ v v = 0 , this is the parallel transport of v \boldsymbol{v} v
With the abstract definition, there may be different covariant derivative. The one we will care about is called the Levi-Civita connection. We will define the covariant derivative by observing the intrinsic definition and using its properties to create an abstract definition.
To save space, I will be using the following notation:
e μ = ∂ ∂ x μ = ∂ μ , \boldsymbol{e_{\mu}} = \frac{\partial}{\partial x^{\mu}} = \partial_{\mu}, e μ = ∂ x μ ∂ = ∂ μ , in particular ∂ μ \partial_{\mu} ∂ μ
The first property is addition and scaling in the direction vector:
∇ a u + b w v = ∇ a u μ ∂ μ + b w μ ∂ μ v = ∇ ( a u μ + b w μ ) ∂ μ v = ( a u μ + b w μ ) ∂ μ v = a u μ ∂ μ v + b w μ ∂ μ v = a ∇ u v + b ∇ w v , \begin{align*} \nabla_{a \boldsymbol{u} + b \boldsymbol{w}} \boldsymbol{v} &= \nabla_{a u^{\mu} \partial_{\mu} + b w^{\mu} \partial_{\mu}} \boldsymbol{v} \\ &= \nabla_{(a u^{\mu} + b w^{\mu}) \partial_{\mu}} \boldsymbol{v} \\ &= (a u^{\mu} + b w^{\mu}) \partial_{\mu} \boldsymbol{v} \\ &= a u^{\mu} \partial_{\mu} \boldsymbol{v} + b w^{\mu} \partial_{\mu} \boldsymbol{v} \\ &= a \nabla_{\boldsymbol{u}} \boldsymbol{v} + b \nabla_{\boldsymbol{w}} \boldsymbol{v}, \end{align*} ∇ a u + b w v = ∇ a u μ ∂ μ + b w μ ∂ μ v = ∇ ( a u μ + b w μ ) ∂ μ v = ( a u μ + b w μ ) ∂ μ v = a u μ ∂ μ v + b w μ ∂ μ v = a ∇ u v + b ∇ w v , also called linearity.
The second property is the covariant derivative of sum of vectors:
∇ u ( v + w ) = ∇ u μ ∂ μ ( v + w ) = u μ ∂ μ ( v + w ) = u μ ∂ μ v + u μ ∂ μ w = ∇ u v + ∇ w v . \begin{align*} \nabla_{\boldsymbol{u}} (\boldsymbol{v} + \boldsymbol{w}) &= \nabla_{u^{\mu} \partial_{\mu}} (\boldsymbol{v} + \boldsymbol{w}) \\ &= u^{\mu} \partial_{\mu} (\boldsymbol{v} + \boldsymbol{w}) \\ &= u^{\mu} \partial_{\mu} \boldsymbol{v} + u^{\mu} \partial_{\mu} \boldsymbol{w} \\ &= \nabla_{\boldsymbol{u}} \boldsymbol{v} + \nabla_{\boldsymbol{w}} \boldsymbol{v}. \end{align*} ∇ u ( v + w ) = ∇ u μ ∂ μ ( v + w ) = u μ ∂ μ ( v + w ) = u μ ∂ μ v + u μ ∂ μ w = ∇ u v + ∇ w v . The third property is the covariant derivative of a scaled vector:
∇ u ( a v ) = ∇ u μ ∂ μ ( a v ) = u μ ∂ μ ( a v ) = ( u μ ∂ μ a ) v + a u μ ∂ μ v = ( ∇ u a ) v + a ( ∇ u v ) . \begin{align*} \nabla_{\boldsymbol{u}} (a \boldsymbol{v}) &= \nabla_{u^{\mu} \partial_{\mu}} (a \boldsymbol{v}) \\ &= u^{\mu} \partial_{\mu} (a \boldsymbol{v}) \\ &= (u^{\mu} \partial_{\mu} a) \boldsymbol{v} + a u^{\mu} \partial_{\mu} \boldsymbol{v} \\ &= (\nabla_{\boldsymbol{u}} a) \boldsymbol{v} + a (\nabla_{\boldsymbol{u}} \boldsymbol{v}). \end{align*} ∇ u ( a v ) = ∇ u μ ∂ μ ( a v ) = u μ ∂ μ ( a v ) = ( u μ ∂ μ a ) v + a u μ ∂ μ v = ( ∇ u a ) v + a ( ∇ u v ) . And the covariant derivative of scalar in a coordinate direction is just the partial derivative:
∇ ∂ μ a = ∂ a ∂ x μ . \nabla_{\partial_{\mu}} a = \frac{\partial a}{\partial x^{\mu}}. ∇ ∂ μ a = ∂ x μ ∂ a . To put the properties together:
∇ a u + b w v = a ∇ u v + b ∇ w v , ∇ u ( v + w ) = ∇ u v + ∇ w v , ∇ u ( a v ) = ( ∇ u v ) a + a ( ∇ u v ) , ∇ ∂ μ a = ∂ a ∂ x μ , \begin{align*} \nabla_{a \boldsymbol{u} + b \boldsymbol{w}} \boldsymbol{v} &= a \nabla_{\boldsymbol{u}} \boldsymbol{v} + b \nabla_{\boldsymbol{w}} \boldsymbol{v}, \\ \nabla_{\boldsymbol{u}} (\boldsymbol{v} + \boldsymbol{w}) &= \nabla_{\boldsymbol{u}} \boldsymbol{v} + \nabla_{\boldsymbol{w}} \boldsymbol{v}, \\ \nabla_{\boldsymbol{u}} (a \boldsymbol{v}) &= (\nabla_{\boldsymbol{u}} \boldsymbol{v}) a + a (\nabla_{\boldsymbol{u}} \boldsymbol{v}), \\ \nabla_{\partial_{\mu}} a &= \frac{\partial a}{\partial x^{\mu}}, \end{align*} ∇ a u + b w v ∇ u ( v + w ) ∇ u ( a v ) ∇ ∂ μ a = a ∇ u v + b ∇ w v , = ∇ u v + ∇ w v , = ( ∇ u v ) a + a ( ∇ u v ) , = ∂ x μ ∂ a , so a covariant derivative ∇ _ _ \nabla_{\_}\ \_ ∇ _ _
In intrinsic geometry, we have defined the partial derivative of basis vector with respect to a coordinate as follows:
∂ e μ ∂ x ν = Γ σ μ ν e σ , \frac{\partial \boldsymbol{e_{\mu}}}{\partial x^{\nu}} = \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}}, ∂ x ν ∂ e μ = Γ σ μν e σ , and the abstract version of this would be:
∇ e ν e μ = Γ σ ν μ e σ , \nabla_{\boldsymbol{e_{\nu}}} \boldsymbol{e_{\mu}} = \Gamma^{\sigma}{}_{\nu \mu} \boldsymbol{e_{\sigma}}, ∇ e ν e μ = Γ σ νμ e σ , where the Christoffel symbols are also sometimes called the connection coefficients. Note that the order in the lower indices of the Christoffel symbols does matter. So generally:
Γ σ ν μ ≠ Γ σ μ ν . \Gamma^{\sigma}{}_{\nu \mu} \neq \Gamma^{\sigma}{}_{\mu \nu}. Γ σ νμ = Γ σ μν . Turns out that the following conditions are not enough to solve for unique connection coefficients:
∇ a u + b w v = a ∇ u v + b ∇ w v , ∇ u ( v + w ) = ∇ u v + ∇ w v , ∇ u ( a v ) = ( ∇ u v ) a + a ( ∇ u v ) , ∇ ∂ μ a = ∂ a ∂ x μ , ∇ e ν e μ = Γ σ ν μ e σ . \begin{align*} \nabla_{a \boldsymbol{u} + b \boldsymbol{w}} \boldsymbol{v} &= a \nabla_{\boldsymbol{u}} \boldsymbol{v} + b \nabla_{\boldsymbol{w}} \boldsymbol{v}, \\ \nabla_{\boldsymbol{u}} (\boldsymbol{v} + \boldsymbol{w}) &= \nabla_{\boldsymbol{u}} \boldsymbol{v} + \nabla_{\boldsymbol{w}} \boldsymbol{v}, \\ \nabla_{\boldsymbol{u}} (a \boldsymbol{v}) &= (\nabla_{\boldsymbol{u}} \boldsymbol{v}) a + a (\nabla_{\boldsymbol{u}} \boldsymbol{v}), \\ \nabla_{\partial_{\mu}} a &= \frac{\partial a}{\partial x^{\mu}}, \\ \nabla_{\boldsymbol{e_{\nu}}} \boldsymbol{e_{\mu}} &= \Gamma^{\sigma}{}_{\nu \mu} \boldsymbol{e}_{\sigma}. \end{align*} ∇ a u + b w v ∇ u ( v + w ) ∇ u ( a v ) ∇ ∂ μ a ∇ e ν e μ = a ∇ u v + b ∇ w v , = ∇ u v + ∇ w v , = ( ∇ u v ) a + a ( ∇ u v ) , = ∂ x μ ∂ a , = Γ σ νμ e σ . To get the unique solution for the connection coefficients, we have to introduce two new properties. The first is the torsion-free property:
∇ w v − ∇ v w = [ v , w ] , \nabla_{\boldsymbol{w}} \boldsymbol{v} - \nabla_{\boldsymbol{v}} \boldsymbol{w} = [\boldsymbol{v}, \boldsymbol{w}], ∇ w v − ∇ v w = [ v , w ] , where [ v , w ] [\boldsymbol{v}, \boldsymbol{w}] [ v , w ]
[ v , w ] = v ( w ) − w ( v ) , [\boldsymbol{v}, \boldsymbol{w}] = \boldsymbol{v} (\boldsymbol{w}) - \boldsymbol{w} (\boldsymbol{v}), [ v , w ] = v ( w ) − w ( v ) , and for our specific case, where the vectors are partial derivative operators (and the order of partial differentiation does not matter):
[ v , w ] = v μ ∂ μ ( w ν ∂ ν ) − w μ ∂ μ ( v ν ∂ ν ) = v μ ∂ μ w ν ∂ ν + v μ w ν ∂ μ ∂ ν − w μ ∂ μ v ν ∂ ν − w μ v ν ∂ μ ∂ ν = v μ ∂ μ w ν ∂ ν − v μ ∂ μ w ν ∂ ν + v μ w ν ∂ μ ∂ ν − w μ v ν ∂ μ ∂ ν = v μ w ν ∂ μ ∂ ν − w μ v ν ∂ μ ∂ ν = 0 , \begin{align*} [\boldsymbol{v}, \boldsymbol{w}] &= v^{\mu} \partial_{\mu} (w^{\nu} \partial_{\nu}) - w^{\mu} \partial_{\mu} (v^{\nu} \partial_{\nu}) \\ &= v^{\mu} \partial_{\mu} w^{\nu} \partial_{\nu} + v^{\mu} w^{\nu} \partial_{\mu} \partial_{\nu} - w^{\mu} \partial_{\mu} v^{\nu} \partial_{\nu} - w^{\mu} v^{\nu} \partial_{\mu} \partial_{\nu} \\ &= v^{\mu} \partial_{\mu} w^{\nu} \partial_{\nu} - v^{\mu} \partial_{\mu} w^{\nu} \partial_{\nu} + v^{\mu} w^{\nu} \partial_{\mu} \partial_{\nu} - w^{\mu} v^{\nu} \partial_{\mu} \partial_{\nu} \\ &= v^{\mu} w^{\nu} \partial_{\mu} \partial_{\nu} - w^{\mu} v^{\nu} \partial_{\mu} \partial_{\nu} \\ &= 0, \end{align*} [ v , w ] = v μ ∂ μ ( w ν ∂ ν ) − w μ ∂ μ ( v ν ∂ ν ) = v μ ∂ μ w ν ∂ ν + v μ w ν ∂ μ ∂ ν − w μ ∂ μ v ν ∂ ν − w μ v ν ∂ μ ∂ ν = v μ ∂ μ w ν ∂ ν − v μ ∂ μ w ν ∂ ν + v μ w ν ∂ μ ∂ ν − w μ v ν ∂ μ ∂ ν = v μ w ν ∂ μ ∂ ν − w μ v ν ∂ μ ∂ ν = 0 , so the torsion-free property is simplified:
∇ w v = ∇ v w . \nabla_{\boldsymbol{w}} \boldsymbol{v} = \nabla_{\boldsymbol{v}} \boldsymbol{w}. ∇ w v = ∇ v w . The torsion property implies the following for the connection coefficients:
∇ e ν e μ = Γ σ ν μ e σ , ∇ e μ e ν = Γ σ μ ν e σ , ∇ e ν e μ = ∇ e μ e ν , Γ σ ν μ e σ = Γ σ μ ν e σ , Γ σ ν μ = Γ σ μ ν . \begin{align*} \nabla_{\boldsymbol{e_{\nu}}} \boldsymbol{e_{\mu}} &= \Gamma^{\sigma}{}_{\nu \mu} \boldsymbol{e_{\sigma}}, \\ \nabla_{\boldsymbol{e_{\mu}}} \boldsymbol{e_{\nu}} &= \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}}, \\ \nabla_{\boldsymbol{e_{\nu}}} \boldsymbol{e_{\mu}} &= \nabla_{\boldsymbol{e_{\mu}}} \boldsymbol{e_{\nu}}, \\ \Gamma^{\sigma}{}_{\nu \mu} \boldsymbol{e_{\sigma}} &= \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}}, \\ \Gamma^{\sigma}{}_{\nu \mu} &= \Gamma^{\sigma}{}_{\mu \nu}. \end{align*} ∇ e ν e μ ∇ e μ e ν ∇ e ν e μ Γ σ νμ e σ Γ σ νμ = Γ σ νμ e σ , = Γ σ μν e σ , = ∇ e μ e ν , = Γ σ μν e σ , = Γ σ μν . The second property is the metric compatibility:
∇ w ( u ⋅ v ) = ( ∇ w u ) ⋅ v + u ⋅ ( ∇ w v ) , \nabla_{\boldsymbol{w}} (\boldsymbol{u} \cdot \boldsymbol{v}) = (\nabla_{\boldsymbol{w}} \boldsymbol{u}) \cdot \boldsymbol{v} + \boldsymbol{u} \cdot (\nabla_{\boldsymbol{w}} \boldsymbol{v}), ∇ w ( u ⋅ v ) = ( ∇ w u ) ⋅ v + u ⋅ ( ∇ w v ) , this may be interpreted that when taking parallel transport of two vectors (∇ w u = ∇ w v = 0 \nabla_{\boldsymbol{w}} \boldsymbol{u} = \nabla_{\boldsymbol{w}} \boldsymbol{v} = \boldsymbol{0} ∇ w u = ∇ w v = 0
∇ w ( u ⋅ v ) = 0 ⋅ v + u ⋅ 0 = 0 , \begin{align*} \nabla_{\boldsymbol{w}} (\boldsymbol{u} \cdot \boldsymbol{v}) &= \boldsymbol{0} \cdot \boldsymbol{v} + \boldsymbol{u} \cdot \boldsymbol{0} \\ &= \boldsymbol{0}, \end{align*} ∇ w ( u ⋅ v ) = 0 ⋅ v + u ⋅ 0 = 0 , implying that the angle between the angle between the vectors stays the same. If the two vectors are the same vector, it implies that the length of the vector stays constant:
∇ w ( ∣ v ∣ 2 ) = ∇ w ( v ⋅ v ) = 0 ⋅ v + u ⋅ v = 0 . \begin{align*} \nabla_{\boldsymbol{w}} (|\boldsymbol{v}|^2) = \nabla_{\boldsymbol{w}} (\boldsymbol{v} \cdot \boldsymbol{v}) &= \boldsymbol{0} \cdot \boldsymbol{v} + \boldsymbol{u} \cdot \boldsymbol{v} \\ &= \boldsymbol{0}. \end{align*} ∇ w ( ∣ v ∣ 2 ) = ∇ w ( v ⋅ v ) = 0 ⋅ v + u ⋅ v = 0 . If we apply metric compatibility on basis vectors, we obtain:
∇ e σ ( e μ ⋅ e ν ) = g μ ν , σ = ( ∇ e σ e μ ) ⋅ e ν + e μ ⋅ ( ∇ e σ e ν ) = Γ λ σ μ e λ ⋅ e ν + Γ λ σ ν e λ ⋅ e μ , = Γ λ σ μ g λ ν + Γ λ σ ν g λ μ \begin{align*} \nabla_{\boldsymbol{e_{\sigma}}} (\boldsymbol{e_{\mu}} \cdot \boldsymbol{e_{\nu}}) = g_{\mu \nu, \sigma} &= (\nabla_{\boldsymbol{e_{\sigma}}} \boldsymbol{e_{\mu}}) \cdot \boldsymbol{e_{\nu}} + \boldsymbol{e_{\mu}} \cdot (\nabla_{\boldsymbol{e_{\sigma}}} \boldsymbol{e_{\nu}}) \\ &= \Gamma^{\lambda}{}_{\sigma \mu} \boldsymbol{e_{\lambda}} \cdot \boldsymbol{e_{\nu}} + \Gamma^{\lambda}{}_{\sigma \nu} \boldsymbol{e_{\lambda}} \cdot \boldsymbol{e_{\mu}}, \\ &= \Gamma^{\lambda}{}_{\sigma \mu} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\sigma \nu} g_{\lambda \mu} \\ \end{align*} ∇ e σ ( e μ ⋅ e ν ) = g μν , σ = ( ∇ e σ e μ ) ⋅ e ν + e μ ⋅ ( ∇ e σ e ν ) = Γ λ σ μ e λ ⋅ e ν + Γ λ σ ν e λ ⋅ e μ , = Γ λ σ μ g λ ν + Γ λ σ ν g λ μ Similar to the intrinsic definition, we swap the indices:
g μ ν , σ = Γ λ μ σ g λ ν + Γ λ ν σ g λ μ , g μ σ , ν = Γ λ μ ν g λ σ + Γ λ ν σ g λ μ , g σ ν , μ = Γ λ μ σ g λ ν + Γ λ μ ν g λ μ , \begin{align*} g_{\mu \nu, \sigma} &= \Gamma^{\lambda}{}_{\mu \sigma} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\nu \sigma} g_{\lambda \mu}, \\ g_{\mu \sigma, \nu} &= \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \sigma} + \Gamma^{\lambda}{}_{\nu \sigma} g_{\lambda \mu}, \\ g_{\sigma \nu, \mu} &= \Gamma^{\lambda}{}_{\mu \sigma} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \mu}, \\ \end{align*} g μν , σ g μ σ , ν g σ ν , μ = Γ λ μ σ g λ ν + Γ λ ν σ g λ μ , = Γ λ μν g λσ + Γ λ ν σ g λ μ , = Γ λ μ σ g λ ν + Γ λ μν g λ μ , remember, we are allowed to swap indices in the connection coefficients because of the torsion free property. We can now derive the connection coefficients:
g μ ν , σ + g μ σ , ν − g σ ν , μ = 2 Γ λ ν σ g λ μ , 1 2 g μ ρ ( g μ ν , σ + g μ σ , ν − g σ ν , μ ) = Γ λ ν σ g λ μ g μ ρ , Γ ρ ν σ = 1 2 g μ ρ ( g μ ν , σ + g μ σ , ν − g σ ν , μ ) , = 1 2 g μ ρ ( ∂ g μ ν ∂ x σ + ∂ g μ σ ∂ x ν − ∂ g σ ν ∂ x μ ) , \begin{align*} g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} - g_{\sigma \nu, \mu} &= 2\Gamma^{\lambda}{}_{\nu \sigma} g_{\lambda \mu}, \\ \frac{1}{2} g^{\mu \rho} (g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} - g_{\sigma \nu, \mu}) &= \Gamma^{\lambda}{}_{\nu \sigma} g_{\lambda \mu} g^{\mu \rho}, \\ \Gamma^{\rho}{}_{\nu \sigma} &= \frac{1}{2} g^{\mu \rho} (g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} - g_{\sigma \nu, \mu}), \\ &= \frac{1}{2} g^{\mu \rho} \left(\frac{\partial g_{\mu \nu}}{\partial x^{\sigma}} + \frac{\partial g_{\mu \sigma}}{\partial x^{\nu}} - \frac{\partial g_{\sigma \nu}}{\partial x^{\mu}}\right), \end{align*} g μν , σ + g μ σ , ν − g σ ν , μ 2 1 g μ ρ ( g μν , σ + g μ σ , ν − g σ ν , μ ) Γ ρ ν σ = 2 Γ λ ν σ g λ μ , = Γ λ ν σ g λ μ g μ ρ , = 2 1 g μ ρ ( g μν , σ + g μ σ , ν − g σ ν , μ ) , = 2 1 g μ ρ ( ∂ x σ ∂ g μν + ∂ x ν ∂ g μ σ − ∂ x μ ∂ g σ ν ) , and the covariant derivative that uses these particular connection coefficients is called the Levi-Civita connection.
The fundamental theorem of Riemann geometry states that on any Riemannian manifold, there is a unique connection that is torsion-free and has metric compatibility - Levi-Civita connection.
There are other connection coefficients. One may be the case where all the connection coefficients Γ ~ ρ μ σ = 0 \tilde{\Gamma}^{\rho}{}_{\mu \sigma} = 0 Γ ~ ρ μ σ = 0 v 0 \boldsymbol{v_0} v 0
∇ d d λ v = 0 , ∇ d d λ v = d v d λ = d x μ d λ ∂ ∂ x μ ( v ν e ν ) = d x μ d λ ( ∂ v ν ∂ x μ e ν + v ν ∂ e ν ∂ x μ ) = d x μ d λ ∂ v σ ∂ x μ e σ + v ν d x μ d λ ∂ e ν ∂ x μ = d v σ d λ e σ + v ν d x μ d λ Γ σ ν μ e σ = ( d v σ d λ + v ν d x μ d λ Γ σ ν μ ) e σ = 0 , \begin{align*} \nabla_{\frac{d}{d\lambda}} \boldsymbol{v} &= \boldsymbol{0}, \\ \nabla_{\frac{d}{d\lambda}} \boldsymbol{v} &= \frac{d\boldsymbol{v}}{d\lambda} \\ &= \frac{d x^{\mu}}{d \lambda} \frac{\partial}{\partial x^{\mu}} (v^{\nu} \boldsymbol{e_{\nu}}) \\ &= \frac{d x^{\mu}}{d \lambda} \left(\frac{\partial v^{\nu}}{\partial x^{\mu}} \boldsymbol{e_{\nu}} + v^{\nu} \frac{\partial \boldsymbol{e_{\nu}}}{\partial x^{\mu}}\right) \\ &= \frac{d x^{\mu}}{d \lambda} \frac{\partial v^{\sigma}}{\partial x^{\mu}} \boldsymbol{e_{\sigma}} + v^{\nu} \frac{d x^{\mu}}{d \lambda} \frac{\partial \boldsymbol{e_{\nu}}}{\partial x^{\mu}} \\ &= \frac{d v^{\sigma}}{d \lambda} \boldsymbol{e_{\sigma}} + v^{\nu} \frac{d x^{\mu}}{d \lambda} \Gamma^{\sigma}{}_{\nu \mu} \boldsymbol{e_{\sigma}} \\ &= \left(\frac{d v^{\sigma}}{d \lambda} + v^{\nu} \frac{d x^{\mu}}{d \lambda} \Gamma^{\sigma}{}_{\nu \mu}\right) \boldsymbol{e_{\sigma}} \\ &= \boldsymbol{0}, \end{align*} ∇ d λ d v ∇ d λ d v = 0 , = d λ d v = d λ d x μ ∂ x μ ∂ ( v ν e ν ) = d λ d x μ ( ∂ x μ ∂ v ν e ν + v ν ∂ x μ ∂ e ν ) = d λ d x μ ∂ x μ ∂ v σ e σ + v ν d λ d x μ ∂ x μ ∂ e ν = d λ d v σ e σ + v ν d λ d x μ Γ σ νμ e σ = ( d λ d v σ + v ν d λ d x μ Γ σ νμ ) e σ = 0 , and since the connection coefficients are zero:
d v σ d λ e σ = 0 , v σ = C σ , \begin{align*} \frac{d v^{\sigma}}{d \lambda} \boldsymbol{e_{\sigma}} &= \boldsymbol{0}, \\ v^{\sigma} &= C^{\sigma}, \end{align*} d λ d v σ e σ v σ = 0 , = C σ , where C σ C^{\sigma} C σ
v = v 0 . \boldsymbol{v} = \boldsymbol{v_0}. v = v 0 . For example, for a curve parametrized by θ = π 4 \theta = \frac{\pi}{4} θ = 4 π ϕ = λ \phi = \lambda ϕ = λ
and there are many more connections.
For a covariant derivative of a vector along another vector is equal to:
∇ u v = ∇ u μ e μ ( v ν e ν ) = u μ ( ( ∇ e μ v ν ) e ν + v ν ( ∇ e μ e ν ) ) = u μ ( v ν ∂ x μ e ν + v ν Γ σ μ ν e σ ) = u μ ( v σ ∂ x μ e σ + v ν Γ σ μ ν e σ ) = u μ ( v σ ∂ x μ + v ν Γ σ μ ν ) e σ . \begin{align*} \nabla_{\boldsymbol{u}} \boldsymbol{v} &= \nabla_{u^{\mu} \boldsymbol{e_{\mu}}} (v^{\nu} \boldsymbol{e_{\nu}}) \\ &= u^{\mu} \left((\nabla_{\boldsymbol{e_{\mu}}} v^{\nu}) \boldsymbol{e_{\nu}} + v^{\nu} (\nabla_{\boldsymbol{e_{\mu}}} \boldsymbol{e_{\nu}})\right) \\ &= u^{\mu} \left(\frac{v^{\nu}}{\partial x^{\mu}} \boldsymbol{e_{\nu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}}\right) \\ &= u^{\mu} \left(\frac{v^{\sigma}}{\partial x^{\mu}} \boldsymbol{e_{\sigma}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}}\right) \\ &= u^{\mu} \left(\frac{v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{e_{\sigma}}. \end{align*} ∇ u v = ∇ u μ e μ ( v ν e ν ) = u μ ( ( ∇ e μ v ν ) e ν + v ν ( ∇ e μ e ν ) ) = u μ ( ∂ x μ v ν e ν + v ν Γ σ μν e σ ) = u μ ( ∂ x μ v σ e σ + v ν Γ σ μν e σ ) = u μ ( ∂ x μ v σ + v ν Γ σ μν ) e σ . So to summarize, the properties of the covariant derivative connection are as follows:
∇ a u + b w v = a ∇ u v + b ∇ w v , ∇ u ( v + w ) = ∇ u v + ∇ w v , ∇ u ( a v ) = ( ∇ u v ) a + a ( ∇ u v ) , ∇ ∂ μ a = ∂ a ∂ x μ , ∇ e ν e μ = Γ σ ν μ e σ . \begin{align*} \nabla_{a \boldsymbol{u} + b \boldsymbol{w}} \boldsymbol{v} &= a \nabla_{\boldsymbol{u}} \boldsymbol{v} + b \nabla_{\boldsymbol{w}} \boldsymbol{v}, \\ \nabla_{\boldsymbol{u}} (\boldsymbol{v} + \boldsymbol{w}) &= \nabla_{\boldsymbol{u}} \boldsymbol{v} + \nabla_{\boldsymbol{w}} \boldsymbol{v}, \\ \nabla_{\boldsymbol{u}} (a \boldsymbol{v}) &= (\nabla_{\boldsymbol{u}} \boldsymbol{v}) a + a (\nabla_{\boldsymbol{u}} \boldsymbol{v}), \\ \nabla_{\partial_{\mu}} a &= \frac{\partial a}{\partial x^{\mu}}, \\ \nabla_{\boldsymbol{e_{\nu}}} \boldsymbol{e_{\mu}} &= \Gamma^{\sigma}{}_{\nu \mu} \boldsymbol{e_{\sigma}}. \end{align*} ∇ a u + b w v ∇ u ( v + w ) ∇ u ( a v ) ∇ ∂ μ a ∇ e ν e μ = a ∇ u v + b ∇ w v , = ∇ u v + ∇ w v , = ( ∇ u v ) a + a ( ∇ u v ) , = ∂ x μ ∂ a , = Γ σ νμ e σ . The Levi-Civita has two special properties - torsion-free and metric compatibility:
∇ w v = ∇ v w , ∇ w ( u ⋅ v ) = ( ∇ w u ) ⋅ v + u ⋅ ( ∇ w v ) , \begin{align*} \nabla_{\boldsymbol{w}} \boldsymbol{v} &= \nabla_{\boldsymbol{v}} \boldsymbol{w}, \\ \nabla_{\boldsymbol{w}} (\boldsymbol{u} \cdot \boldsymbol{v}) &= (\nabla_{\boldsymbol{w}} \boldsymbol{u}) \cdot \boldsymbol{v} + \boldsymbol{u} \cdot (\nabla_{\boldsymbol{w}} \boldsymbol{v}), \end{align*} ∇ w v ∇ w ( u ⋅ v ) = ∇ v w , = ( ∇ w u ) ⋅ v + u ⋅ ( ∇ w v ) , and the Levi-Civita connection coefficients are equal to:
Γ ρ ν σ = 1 2 g μ ρ ( g μ ν , σ + g μ σ , ν − g σ ν , μ ) , = 1 2 g μ ρ ( ∂ g μ ν ∂ x σ + ∂ g μ σ ∂ x ν − ∂ g σ ν ∂ x μ ) . \begin{align*} \Gamma^{\rho}{}_{\nu \sigma} &= \frac{1}{2} g^{\mu \rho} (g_{\mu \nu, \sigma} + g_{\mu \sigma, \nu} - g_{\sigma \nu, \mu}), \\ &= \frac{1}{2} g^{\mu \rho} \left(\frac{\partial g_{\mu \nu}}{\partial x^{\sigma}} + \frac{\partial g_{\mu \sigma}}{\partial x^{\nu}} - \frac{\partial g_{\sigma \nu}}{\partial x^{\mu}}\right). \end{align*} Γ ρ ν σ = 2 1 g μ ρ ( g μν , σ + g μ σ , ν − g σ ν , μ ) , = 2 1 g μ ρ ( ∂ x σ ∂ g μν + ∂ x ν ∂ g μ σ − ∂ x μ ∂ g σ ν ) . And remember, the order of indices in the Christoffel symbols matters in connections without the torsion free property. So generally:
∇ e ν e μ = Γ σ ν μ e σ ≠ Γ σ μ ν e σ . \nabla_{\boldsymbol{e_{\nu}}} \boldsymbol{e_{\mu}} = \Gamma^{\sigma}{}_{\nu \mu} \boldsymbol{e_{\sigma}} \neq \Gamma^{\sigma}{}_{\mu \nu} \boldsymbol{e_{\sigma}}. ∇ e ν e μ = Γ σ νμ e σ = Γ σ μν e σ . And for a covariant derivative of a vector along another vector is equal to:
∇ u v = u μ ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) e σ , \nabla_{\boldsymbol{u}} \boldsymbol{v} = u^{\mu} \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{e_{\sigma}}, ∇ u v = u μ ( ∂ x μ ∂ v σ + v ν Γ σ μν ) e σ , and for the covariant derivative along a basis vector:
∇ e μ v = ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) e σ . \nabla_{\boldsymbol{e_{\mu}}} \boldsymbol{v} = \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{e_{\sigma}}. ∇ e μ v = ( ∂ x μ ∂ v σ + v ν Γ σ μν ) e σ . Recall the following property of covectors:
ϵ μ ( e ν ) = δ ν μ , \epsilon^{\mu} (\boldsymbol{e_{\nu}}) = \delta^{\mu}_{\nu}, ϵ μ ( e ν ) = δ ν μ , or when expressed as differential:
d x μ ( ∂ ∂ x ν ) = ∂ x μ ∂ x ν = δ ν μ . dx^{\mu} \left(\frac{\partial}{\partial x^{\nu}}\right) = \frac{\partial x^{\mu}}{\partial x^{\nu}} = \delta^{\mu}_{\nu}. d x μ ( ∂ x ν ∂ ) = ∂ x ν ∂ x μ = δ ν μ . Taking the covariant derivative of a covector a a a
∇ ∂ μ ( α ) = ∇ ∂ μ ( α ν ϵ ν ) = ( ∇ ∂ μ α ν ) ϵ ν + α ν ( ∇ ∂ μ ϵ ν ) = ∂ α σ ∂ x μ ϵ σ + α ν Λ ν μ σ ϵ σ = ( ∂ α σ ∂ x μ + α ν Λ ν μ σ ) ϵ σ , \begin{align*} \nabla_{\partial_{\mu}} (\alpha) &= \nabla_{\partial_{\mu}} (\alpha_{\nu} \epsilon^{\nu}) \\ &= (\nabla_{\partial_{\mu}} \alpha_{\nu}) \epsilon^{\nu} + \alpha_{\nu} (\nabla_{\partial_{\mu}} \epsilon^{\nu}) \\ &= \frac{\partial \alpha_{\sigma}}{\partial x^{\mu}} \epsilon^{\sigma} + \alpha_{\nu} \Lambda^{\nu}{}_{\mu \sigma} \epsilon^{\sigma} \\ &= \left(\frac{\partial \alpha_{\sigma}}{\partial x^{\mu}} + \alpha_{\nu} \Lambda^{\nu}{}_{\mu \sigma}\right) \epsilon^{\sigma}, \end{align*} ∇ ∂ μ ( α ) = ∇ ∂ μ ( α ν ϵ ν ) = ( ∇ ∂ μ α ν ) ϵ ν + α ν ( ∇ ∂ μ ϵ ν ) = ∂ x μ ∂ α σ ϵ σ + α ν Λ ν μ σ ϵ σ = ( ∂ x μ ∂ α σ + α ν Λ ν μ σ ) ϵ σ , where:
∇ ∂ μ ϵ ν = Λ ν μ σ ϵ σ . \nabla_{\partial_{\mu}} \epsilon^{\nu} = \Lambda^{\nu}{}_{\mu \sigma} \epsilon^{\sigma}. ∇ ∂ μ ϵ ν = Λ ν μ σ ϵ σ . Consider the covariant of the covector α \alpha α v \boldsymbol{v} v
∇ ∂ μ ( α ( v ) ) = ∇ ∂ μ ( a ⋅ v ) , \nabla_{\partial_{\mu}} (\alpha(\boldsymbol{v})) = \nabla_{\partial_{\mu}} (\boldsymbol{a} \cdot \boldsymbol{v}), ∇ ∂ μ ( α ( v )) = ∇ ∂ μ ( a ⋅ v ) , using the metric compatibility:
∇ ∂ μ ( a ⋅ v ) = ( ∇ ∂ μ a ) ⋅ v + a ⋅ ( ∇ ∂ μ v ) , ∇ ∂ μ ( α ( v ) ) = ( ∇ ∂ μ α ) ( v ) + α ( ∇ ∂ μ v ) , ∇ ∂ μ ( α σ ϵ σ ( v ν e ν ) ) = ( ∂ α σ ∂ x μ + α ν Λ ν μ σ ) ϵ σ ( v ) + α ( ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) e σ ) , ∇ ∂ μ ( α σ v ν ϵ σ ( e ν ) ) = ( ∂ α σ ∂ x μ + α ν Λ ν μ σ ) v σ + ( ∂ v σ ∂ x μ + v ν Γ σ μ ν ) α ( e σ ) , ∇ ∂ μ ( α σ v ν δ ν σ ) = ∂ α σ ∂ x μ v σ + α ν Λ ν μ σ v σ + ∂ v σ ∂ x μ α σ + v ν Γ σ μ ν α σ , ∇ ∂ μ ( α ν v ν ) = ∂ α ν ∂ x μ v ν + α ν ∂ v ν ∂ x μ + α ν Λ ν μ σ v σ + v ν Γ σ μ ν α σ = ∇ ∂ μ ( α ν v ν ) + α ν Λ ν μ σ v σ + v ν Γ σ μ ν α σ , 0 = α ν v σ Λ ν μ σ + α σ v ν Γ σ μ ν , α σ v ν Λ σ μ ν = − α σ v ν Γ σ μ ν , Λ σ μ ν = − Γ σ μ ν , \begin{align*} \nabla_{\partial_{\mu}} (\boldsymbol{a} \cdot \boldsymbol{v}) &= (\nabla_{\partial_{\mu}} \boldsymbol{a}) \cdot \boldsymbol{v} + \boldsymbol{a} \cdot (\nabla_{\partial_{\mu}} \boldsymbol{v}), \\ \nabla_{\partial_{\mu}} (\alpha(\boldsymbol{v})) &= (\nabla_{\partial_{\mu}} \alpha) (\boldsymbol{v}) + \alpha(\nabla_{\partial_{\mu}} \boldsymbol{v}), \\ \nabla_{\partial_{\mu}} (\alpha_{\sigma} \epsilon^{\sigma} (v^{\nu} \boldsymbol{e_{\nu}})) &= \left(\frac{\partial \alpha_{\sigma}}{\partial x^{\mu}} + \alpha_{\nu} \Lambda^{\nu}{}_{\mu \sigma}\right) \epsilon^{\sigma} (\boldsymbol{v}) + \alpha \left(\left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \boldsymbol{e_{\sigma}}\right), \\ \nabla_{\partial_{\mu}} (\alpha_{\sigma} v^{\nu} \epsilon^{\sigma} (\boldsymbol{e_{\nu}})) &= \left(\frac{\partial \alpha_{\sigma}}{\partial x^{\mu}} + \alpha_{\nu} \Lambda^{\nu}{}_{\mu \sigma}\right) v^{\sigma} + \left(\frac{\partial v^{\sigma}}{\partial x^{\mu}} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}\right) \alpha(\boldsymbol{e_{\sigma}}), \\ \nabla_{\partial_{\mu}} (\alpha_{\sigma} v^{\nu} \delta^{\sigma}_{\nu}) &= \frac{\partial \alpha_{\sigma}}{\partial x^{\mu}} v^{\sigma} + \alpha_{\nu} \Lambda^{\nu}{}_{\mu \sigma} v^{\sigma} + \frac{\partial v^{\sigma}}{\partial x^{\mu}} \alpha_{\sigma} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu} \alpha_{\sigma}, \\ \nabla_{\partial_{\mu}} (\alpha_{\nu} v^{\nu}) &= \frac{\partial \alpha_{\nu}}{\partial x^{\mu}} v^{\nu} + \alpha_{\nu} \frac{\partial v^{\nu}}{\partial x^{\mu}} + \alpha_{\nu} \Lambda^{\nu}{}_{\mu \sigma} v^{\sigma} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu} \alpha_{\sigma} \\ &= \nabla_{\partial_{\mu}} (\alpha_{\nu} v^{\nu}) + \alpha_{\nu} \Lambda^{\nu}{}_{\mu \sigma} v^{\sigma} + v^{\nu} \Gamma^{\sigma}{}_{\mu \nu} \alpha_{\sigma}, \\ 0 &= \alpha_{\nu} v^{\sigma} \Lambda^{\nu}{}_{\mu \sigma} + \alpha_{\sigma} v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}, \\ \alpha_{\sigma} v^{\nu} \Lambda^{\sigma}{}_{\mu \nu} &= - \alpha_{\sigma} v^{\nu} \Gamma^{\sigma}{}_{\mu \nu}, \\ \Lambda^{\sigma}{}_{\mu \nu} &= - \Gamma^{\sigma}{}_{\mu \nu}, \end{align*} ∇ ∂ μ ( a ⋅ v ) ∇ ∂ μ ( α ( v )) ∇ ∂ μ ( α σ ϵ σ ( v ν e ν )) ∇ ∂ μ ( α σ v ν ϵ σ ( e ν )) ∇ ∂ μ ( α σ v ν δ ν σ ) ∇ ∂ μ ( α ν v ν ) 0 α σ v ν Λ σ μν Λ σ μν = ( ∇ ∂ μ a ) ⋅ v + a ⋅ ( ∇ ∂ μ v ) , = ( ∇ ∂ μ α ) ( v ) + α ( ∇ ∂ μ v ) , = ( ∂ x μ ∂ α σ + α ν Λ ν μ σ ) ϵ σ ( v ) + α ( ( ∂ x μ ∂ v σ + v ν Γ σ μν ) e σ ) , = ( ∂ x μ ∂ α σ + α ν Λ ν μ σ ) v σ + ( ∂ x μ ∂ v σ + v ν Γ σ μν ) α ( e σ ) , = ∂ x μ ∂ α σ v σ + α ν Λ ν μ σ v σ + ∂ x μ ∂ v σ α σ + v ν Γ σ μν α σ , = ∂ x μ ∂ α ν v ν + α ν ∂ x μ ∂ v ν + α ν Λ ν μ σ v σ + v ν Γ σ μν α σ = ∇ ∂ μ ( α ν v ν ) + α ν Λ ν μ σ v σ + v ν Γ σ μν α σ , = α ν v σ Λ ν μ σ + α σ v ν Γ σ μν , = − α σ v ν Γ σ μν , = − Γ σ μν , substituting into the equation for covariant derivative:
∇ ∂ μ ( α ) = ( ∂ α σ ∂ x μ − α ν Γ ν μ σ ) ϵ σ , \nabla_{\partial_{\mu}} (\alpha) = \left(\frac{\partial \alpha_{\sigma}}{\partial x^{\mu}} - \alpha_{\nu} \Gamma^{\nu}{}_{\mu \sigma}\right) \epsilon^{\sigma}, ∇ ∂ μ ( α ) = ( ∂ x μ ∂ α σ − α ν Γ ν μ σ ) ϵ σ , and for the basis covector:
∇ ∂ μ ϵ ν = − Γ ν μ σ ϵ σ . \nabla_{\partial_{\mu}} \epsilon^{\nu} = -\Gamma^{\nu}{}_{\mu \sigma} \epsilon^{\sigma}. ∇ ∂ μ ϵ ν = − Γ ν μ σ ϵ σ . To take the covariant derivative of a tensor, we have to declare the following property:
∇ w ( T ⊗ S ) = ( ∇ w T ) ⊗ S + T ⊗ ( ∇ w S ) . \nabla_{\boldsymbol{w}} (T \otimes S) = (\nabla_{\boldsymbol{w}} T) \otimes S + T \otimes (\nabla_{\boldsymbol{w}} S). ∇ w ( T ⊗ S ) = ( ∇ w T ) ⊗ S + T ⊗ ( ∇ w S ) . Consider the covariant derivative of the metric tensor:
∇ ∂ μ ( g ) = ∇ ∂ μ ( g σ ν ϵ σ ⊗ ϵ ν ) = ∇ ∂ μ ( g σ ν ) ( ϵ σ ⊗ ϵ ν ) + g σ ν ∇ ∂ μ ( ϵ σ ⊗ ϵ ν ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) + g σ ν ( ( ∇ ∂ μ ϵ σ ) ⊗ ϵ ν + ϵ σ ⊗ ( ∇ ∂ μ ϵ ν ) ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) + g σ ν ( − Γ σ μ λ ϵ λ ⊗ ϵ ν − ϵ σ ⊗ Γ ν μ λ ϵ λ ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) + g σ ν ( − Γ σ μ λ ( ϵ λ ⊗ ϵ ν ) − Γ ν μ λ ( ϵ σ ⊗ ϵ λ ) ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) − g σ ν Γ σ μ λ ( ϵ λ ⊗ ϵ ν ) − g σ ν Γ ν μ λ ( ϵ σ ⊗ ϵ λ ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) − g λ ν Γ λ μ σ ( ϵ σ ⊗ ϵ ν ) − g σ λ Γ λ μ ν ( ϵ σ ⊗ ϵ ν ) = ( g σ ν , μ − g λ ν Γ λ μ σ − g σ λ Γ λ μ ν ) ( ϵ σ ⊗ ϵ ν ) . \begin{align*} \nabla_{\partial_{\mu}} (g) &= \nabla_{\partial_{\mu}} (g_{\sigma \nu} \epsilon^{\sigma} \otimes \epsilon^{\nu}) \\ &= \nabla_{\partial_{\mu}} (g_{\sigma \nu}) (\epsilon^{\sigma} \otimes \epsilon^{\nu}) + g_{\sigma \nu} \nabla_{\partial_{\mu}} (\epsilon^{\sigma} \otimes \epsilon^{\nu}) \\ &= g_{\sigma \nu, \mu} (\epsilon^{\sigma} \otimes \epsilon^{\nu}) + g_{\sigma \nu} \left((\nabla_{\partial_{\mu}} \epsilon^{\sigma}) \otimes \epsilon^{\nu} + \epsilon^{\sigma} \otimes (\nabla_{\partial_{\mu}} \epsilon^{\nu})\right) \\ &= g_{\sigma \nu, \mu} (\epsilon^{\sigma} \otimes \epsilon^{\nu}) + g_{\sigma \nu} \left(- \Gamma^{\sigma}{}_{\mu \lambda} \epsilon^{\lambda} \otimes \epsilon^{\nu} - \epsilon^{\sigma} \otimes \Gamma^{\nu}{}_{\mu \lambda} \epsilon^{\lambda}\right) \\ &= g_{\sigma \nu, \mu} (\epsilon^{\sigma} \otimes \epsilon^{\nu}) + g_{\sigma \nu} \left(- \Gamma^{\sigma}{}_{\mu \lambda} (\epsilon^{\lambda} \otimes \epsilon^{\nu}) - \Gamma^{\nu}{}_{\mu \lambda} (\epsilon^{\sigma} \otimes \epsilon^{\lambda})\right) \\ &= g_{\sigma \nu, \mu} (\epsilon^{\sigma} \otimes \epsilon^{\nu}) - g_{\sigma \nu} \Gamma^{\sigma}{}_{\mu \lambda} (\epsilon^{\lambda} \otimes \epsilon^{\nu}) - g_{\sigma \nu} \Gamma^{\nu}{}_{\mu \lambda} (\epsilon^{\sigma} \otimes \epsilon^{\lambda}) \\ &= g_{\sigma \nu, \mu} (\epsilon^{\sigma} \otimes \epsilon^{\nu}) - g_{\lambda \nu} \Gamma^{\lambda}{}_{\mu \sigma} (\epsilon^{\sigma} \otimes \epsilon^{\nu}) - g_{\sigma \lambda} \Gamma^{\lambda}{}_{\mu \nu} (\epsilon^{\sigma} \otimes \epsilon^{\nu}) \\ &= \left(g_{\sigma \nu, \mu} - g_{\lambda \nu} \Gamma^{\lambda}{}_{\mu \sigma} - g_{\sigma \lambda} \Gamma^{\lambda}{}_{\mu \nu}\right) (\epsilon^{\sigma} \otimes \epsilon^{\nu}). \end{align*} ∇ ∂ μ ( g ) = ∇ ∂ μ ( g σ ν ϵ σ ⊗ ϵ ν ) = ∇ ∂ μ ( g σ ν ) ( ϵ σ ⊗ ϵ ν ) + g σ ν ∇ ∂ μ ( ϵ σ ⊗ ϵ ν ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) + g σ ν ( ( ∇ ∂ μ ϵ σ ) ⊗ ϵ ν + ϵ σ ⊗ ( ∇ ∂ μ ϵ ν ) ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) + g σ ν ( − Γ σ μ λ ϵ λ ⊗ ϵ ν − ϵ σ ⊗ Γ ν μ λ ϵ λ ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) + g σ ν ( − Γ σ μ λ ( ϵ λ ⊗ ϵ ν ) − Γ ν μ λ ( ϵ σ ⊗ ϵ λ ) ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) − g σ ν Γ σ μ λ ( ϵ λ ⊗ ϵ ν ) − g σ ν Γ ν μ λ ( ϵ σ ⊗ ϵ λ ) = g σ ν , μ ( ϵ σ ⊗ ϵ ν ) − g λ ν Γ λ μ σ ( ϵ σ ⊗ ϵ ν ) − g σλ Γ λ μν ( ϵ σ ⊗ ϵ ν ) = ( g σ ν , μ − g λ ν Γ λ μ σ − g σλ Γ λ μν ) ( ϵ σ ⊗ ϵ ν ) . We can see a pattern in the connection coefficients. For an ( m , n ) (m, n) ( m , n ) m m m n n n
Recall the metric compatibility:
g μ ν , σ = Γ λ σ μ g λ ν + Γ λ σ ν g λ μ , 0 = g μ ν , σ − Γ λ σ μ g λ ν − Γ λ σ ν g λ μ , 0 = g σ ν , μ − Γ λ μ σ g λ ν − Γ λ μ ν g λ σ , 0 = g σ ν , μ − g λ ν Γ λ μ σ − g σ λ Γ λ μ ν , \begin{align*} g_{\mu \nu, \sigma} &= \Gamma^{\lambda}{}_{\sigma \mu} g_{\lambda \nu} + \Gamma^{\lambda}{}_{\sigma \nu} g_{\lambda \mu}, \\ 0 &= g_{\mu \nu, \sigma} - \Gamma^{\lambda}{}_{\sigma \mu} g_{\lambda \nu} - \Gamma^{\lambda}{}_{\sigma \nu} g_{\lambda \mu}, \\ 0 &= g_{\sigma \nu, \mu} - \Gamma^{\lambda}{}_{\mu \sigma} g_{\lambda \nu} - \Gamma^{\lambda}{}_{\mu \nu} g_{\lambda \sigma}, \\ 0 &= g_{\sigma \nu, \mu} - g_{\lambda \nu} \Gamma^{\lambda}{}_{\mu \sigma} - g_{\sigma \lambda} \Gamma^{\lambda}{}_{\mu \nu}, \\ \end{align*} g μν , σ 0 0 0 = Γ λ σ μ g λ ν + Γ λ σ ν g λ μ , = g μν , σ − Γ λ σ μ g λ ν − Γ λ σ ν g λ μ , = g σ ν , μ − Γ λ μ σ g λ ν − Γ λ μν g λσ , = g σ ν , μ − g λ ν Γ λ μ σ − g σλ Γ λ μν , the right hand side is exactly the same as the covariant derivative of the metric tensor:
∇ ∂ μ ( g ) = ( 0 ) ( ϵ σ ⊗ ϵ ν ) = 0. \nabla_{\partial_{\mu}} (g) = (0) (\epsilon^{\sigma} \otimes \epsilon^{\nu}) = 0. ∇ ∂ μ ( g ) = ( 0 ) ( ϵ σ ⊗ ϵ ν ) = 0. So another way to write metric compatibility is that the covariant derivative of the metric tensor in any direction is zero:
∇ ∂ μ ( g ) = 0. \nabla_{\partial_{\mu}} (g) = 0. ∇ ∂ μ ( g ) = 0.